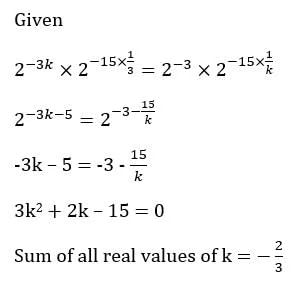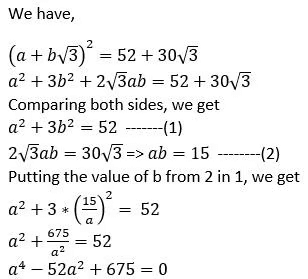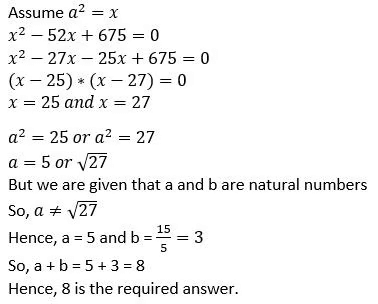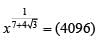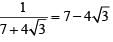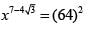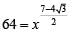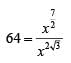Surds & Indices CAT Previous Year Questions with Answer PDF
2024
Q1: The sum of all real values of k for which 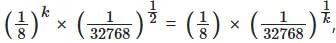 is
is
(a) 2/3
(b) 4/3
(c) -4/3
(d) -2/3
Ans: d
Sol:
Q2: (a + b√3)2 = 52 + 30√3, where a and b are natural numbers, then a + b equals
(a) 9
(b) 7
(c) 8
(d) 10
Ans: c
Sol:
2023
Q1: Let a, b, m and n be natural numbers such that a > 1 and b > 1. If ambn = 144145, then the largest possible value of n mis [2023]
(a) 580
(b) 290
(c) 289
(d) 579
Ans: d
Sol:
It is given that am . bn = 144145, where a > 1 and b > 1.144 can be written as 144 = 24 x 32
Hence, am . bn = 144145 can be written as am . bn = (24 x 32)145 = 2580 x 3290
We know that 3290 is a natural number, which implies it can be written as al, where a > 1
Hence, the least possible value of m is 1. Similarly, the largest value of n is 580.
Hence, the largest value of (n-m) is (580-1) = 579
The correct option is D
Q2: Let n be any natural number such that 5n-1 < 3n+1. Then, the least integer value of m that satisfies 3n+1 < 2n+m for each such n, is [2023]
Ans: 5
Sol: It is given that 5n-1 < 3n+1, where n is a natural number. By inspection, we can say that the inequality holds when n = 1, 2, 3 4, and 5.
Now, we need to find the least integer value of m that satisfies 3n+1 < 2n+m
For, n =1, the least integer value of m is 2.
For, n = 2, the least integer value of m is 3
For, n = 3, the least integer value of m is 4.
For, n = 4, the least integer value of m is 4.
For, n= 5, the least integer value of m is 5.
Hence, the least integer value of m such that for all the values of n, the equation holds is 5.
2022
Q1: Let A be the largest positive integer that divides all the numbers of the form 3k + 4k + 5k, and B be the largest positive integer that divides all the numbers of the form 4k + 3(4k) + 4k+2, where k is any positive integer. Then (A + B) equals [2022]
Ans: 82
Sol: A is the HCF of 3k + 4k + 5k for different values of k.
For k = 1, value is 12
For k = 2, value is 50
For k = 3, value is 216
HCF is 2. Therefore, A = 2
4k + 3 (4k) + 4k+2 = 4k (1 + 3) + 4k+2 = 4k+1 + 4k+2 = 4k+1 (1 + 4) = 5 · 4k+1
HCF of the values is when k = 1, i.e. 5*16 = 80
Therefore, B = 80
A + B = 82
2020
Q1: If x = ( 4096)7+4√3 , then which of the following equals 64? [2020]
(a) 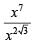
(b) 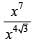
(c) 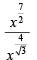
(d) 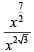
Ans: d
Sol: x = ( 4096)7+4√3
On rationalizing 7+4√3, we get
∴
∴
=
Q2: If a, b, c are non-zero and 14a = 36b = 84c, then 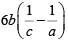 is equal to [2020]
is equal to [2020]
Ans: 3
Sol: Let 14a = 36b = 84c = k
⇒
Similarly,
Required answer,
=
= 3
|
184 videos|212 docs|103 tests
|
FAQs on Surds & Indices CAT Previous Year Questions with Answer PDF
| 1. What is the difference between a surd and an index? |  |
| 2. How can surds be simplified? |  |
| 3. What are some common properties of indices? |  |
| 4. How are surds and indices used in real-life applications? |  |
| 5. Can surds and indices be used in calculus? |  |