Tips and Tricks: Number System | Quantitative Aptitude (Quant) - CAT PDF Download
| Table of contents |

|
| Introduction |

|
| HCF & LCM |

|
| Prime and Composite Numbers |

|
| Theorems on Prime Numbers |

|
| Some Tricks to Remember |

|
| Divisibility |

|
| Cyclicity |

|
| Number of Zeroes |

|
Introduction
Number Systems is the most important topic in the quantitative section. It is a very vast topic and a significant number of questions can be seen based on this topic in many competitive exams. Learning simple tricks like divisibility rules, HCF and LCM, prime numbers and remainder theorems can help improve the score drastically.
HCF & LCM
- HCF * LCM of two numbers = Product of two numbers.
- The greatest number dividing a, b and c such that (a<b<c) leaving the same remainder each time is the HCF of (c-b), (c-a), (b-a).
- If a number, N, is divisible by X and Y and HCF(X,Y). Then, N is divisible by X * Y.
Prime and Composite Numbers
- Prime numbers are numbers with only two factors, 1 and the number itself.
- Composite numbers are numbers with more than 2 factors. Examples are 4, 6, 8, 9.
- 0 and 1 are neither composite nor prime.
- There are 25 prime numbers less than 100.
Properties of Prime numbers
- To check if n is a prime number, list all prime factors less than or equal to √n. If none of the prime factors can divide n then n is a prime number.
- For any integer a and prime number p, ap-a is always divisible by p.
- All prime number greater than 2 and 3 can be written in the form of 6k+1 or 6k-1.
- If a and b are coprime then ab-1 mod b=1.
Theorems on Prime Numbers
- Fermat's Theorem: Remainder of a(p-1) when divided by p is 1, where p is a prime.
- Wilson's Theorem: Remainder when (p-1)! is divided by p is (p-1) where p is a prime
- Remainder Theorem
- If a, b, c are the prime factors of N such that N= ap* bq*cr Then the number o f numbers less than N and co-prime to N is ϕ(N)= N (1 - 1/a) (1 - 1/b) (1 - 1/c).
- This function is known as the Euler's totient function.
Euler's theorem
- If M & N are co-prime to each other than remainder when Mϕ(N) is divided by N is 1.
- Highest power of n in m! is

Example: Highest power of 7 in 100!
Some Tricks to Remember
- To find the number of zeroes in n! find the highest power of 5 in n!
- If all possible permutations of n distinct digits are added together the sum = (n-1)! * (sum of n digits) * (11111... n times)
- If the number can be represented as N = ap* bq*cr... then number of factors the is (p+1) * (q+1)* (r+1)
- Sum of the factors =

- If the number of factors are odd then N is a perfect square.
- If there are n factors, then the number of pairs of factors would be n/2.
- If N is a perfect square then number of pairs (including the square root) is (n+1)/2.
- If the number can be expressed as N = 2p * aq * br ... where the power of 2 is p and a, b are prime numbers. Then the number of even factors of N = p (1+q) (1+r)... The number of odd factors of N = (1+q) (1+r)…
- Number of positive integral solutions of the equation x2 + y2 = k is given by
Total number of factors of k/2 (If k is odd but not a perfect square) (If k is odd and a perfect square)
(If k is odd and a perfect square) (If k is even and not a perfect square)
(If k is even and not a perfect square) (If it is even and a perfect square)
(If it is even and a perfect square) - Number of digits in ab = [ b logm (a) ] + 1 ; where m is the base of the number and [.] denotes greatest integer function.
- Even number which is not a multiple of 4, can never be expressed as a difference of 2 perfect squares.
- Sum of first n odd numbers is n2.
- Sum of first n even numbers is n(n+1).
- The product of the factors of N is given by Na/2, where a is the number of factors.
- The last two digits of a2, (50 - a)2, (50 + a)2, (100 - a2). . . . . are the same.
- If the number is written as 210n.
- When n is odd, the last 2 digits are 24.
- When n is even, the last 2 digits are 76.
Divisibility
- Divisibility by 2: Last digit divisible by 2
- Divisibility by 4: Last two digits divisible by 4
- Divisibility by 8: Last three digits divisible by 8
- Divisibility by 16: Last four digit divisible by 16
- Divisibility by 3: Sum of digits divisible by 3
- Divisibility by 9: Sum of digits divisible by 9
- Divisibility by 27: Sum of blocks of 3 (taken right to left) divisible by 27
- Divisibility by 7: Remove the last digit, double it and subtract it from the truncated original number, check if number is divisible by 7
- Divisibility by 11: (sum of odd digits) - (sum of even digits) should be 0 or divisible by 11
Divisibility properties
- For composite divisors, check if the number is divisible by the factors individually.
- Hence to check if a number is divisible by 6 it must be divisible by 2 and 3.
- The equation an - bn is always divisible by a-b. If n is even it is divisible by a + b. If n is odd it is not divisible by a + b.
- The equation an + bn is divisible by a+b if n is odd. If n is even it is not divisible by a+b.
- Converting from decimal to base b. Let R1 + R2 .. be the remainder left after repeatedly dividing the number with b. Hence, the number in base b is given by ... R2 R1.
- Converting from base b to decimal - multiply each digit of the number with a power of b starting with the rightmost digit and b 0 .
- A decimal number is divisible by b-1 only if the sum of the digits of the number when written in base b are divisible by b-1.
Cyclicity
To find the last digit of a n find the cyclicity of a. For Ex. if a=2, we see that
- 21 = 2
- 22 = 4
- 23 = 8
- 24 = 16
- 25 = 32
Hence, the last digit of 2 repeats after every 4th power. Hence cyclicity of 2 = 4. Hence if we have to find the last digit of an, The steps are:
- Find the cyclicity of a, say it is x 2.
- Find the remainder when n is divided by x, say remainder r
- Find a r if r > 0 and ax when r = 0
- (a + b)(a — b) = (a2 — b2)
- (a + b)2 = (a2 + b2 + 2 ab)
- (a — b)2 = (a2 + b2 — 2ab)
- (a + b + c)2 = (a2 + b2 + 2(ab + be + ca))
- (a + b + c)2= (a2 + b2 + 2 (ab + bc + ca))
- (a3 + b3) = (a + b) (a2 — ab + b2)
- (a3 + b3) = (a + b) (a2 — ab + b2)
- (a3 + b3) = (a + b) (a2 — ab + b2)
- (a3 + b3 + c3 — 3abc) = (a + b) (a2 + b2 + c2 — ab — bc — ac)
- When a + b + c = 0, then a3 + b3 + c3 = 3abc
Number of Zeroes
1. Number of zeroes in an expression
- Zeroes are formed by a combination of 2 × 5.
- Hence, the number of zeroes will depend on the number of pairs of 2’s and 5’s that can be formed.
2. Finding the number of zeroes in a factorial value
- Method 1: Suppose you had to find the number of zeroes in 6!. 6! = 6 × 5 × 4 × 3 × 2 × 1 = (3 × 2) × (5) × (2 × 2) × (3) × (2) × (1).
Counting the number of 5 will give the answer. - Method 2 : For finding the zeroes in 6! we use
 So we get 1 as the answer as all divisions after the first term in the series are in decimals which we ignore.
So we get 1 as the answer as all divisions after the first term in the series are in decimals which we ignore.
|
191 videos|131 docs|110 tests
|
FAQs on Tips and Tricks: Number System - Quantitative Aptitude (Quant) - CAT
| 1. What is the difference between HCF and LCM? |  |
| 2. How can I identify prime and composite numbers? |  |
| 3. What are some important properties of prime numbers? |  |
| 4. What are the key theorems related to prime numbers? |  |
| 5. How does the concept of divisibility apply to HCF and LCM? |  |

 (If k is odd and a perfect square)
(If k is odd and a perfect square) (If k is even and not a perfect square)
(If k is even and not a perfect square)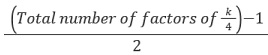 (If it is even and a perfect square)
(If it is even and a perfect square) So we get 1 as the answer as all divisions after the first term in the series are in decimals which we ignore.
So we get 1 as the answer as all divisions after the first term in the series are in decimals which we ignore.

















