Arun Sharma Test: Averages- 1 - CAT MCQ
15 Questions MCQ Test Quantitative Aptitude (Quant) - Arun Sharma Test: Averages- 1
Total expenses of a boarding house are partly fixed and partly varying linearly with the number of boarders. The average expense per boarder is Rs. 700 when there are 25 boarders and Rs. 600 when there are 50 boarders. What is the average expense per boarder when there are 100 boarders?
The average age of a class of 30 students and a teacher reduces by 0.5 years if we exclude the teacher. If the initial average is 14 years, find the age of the class teacher.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The average of a batsman after 25 innings was 56 runs per innings. If after the 26th inning his average increased by 2 runs, then what was his score in the 26 inning?
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes, answer the questions that follow:
A - Highest score 22, Lowest score 18
B - Highest score 31, Lowest score 23
C - Highest score 33, Lowest score 26
If five students are transferred from A to B. What will happen to the average score of B?
Read the following:
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes, answer the questions that follow:
A - Highest score 22, Lowest score 18
B - Highest score 31, Lowest score 23
C - Highest score 33, Lowest score 26
In a transfer of 5 students from A to C
What will happen to the average score of C?
In 2001 there were 6 members in Barney’s family and their average age was 28 years. He got married between 2001 and 2004 and in 2004 there was an addition of a child in his family. In 2006, the average age of his family was 32 years. What is the present age (in 2006) of Barney’s wife (in years) is:
The weight of a metal piece as calculated by the average of 7 different experiments is 53.735 gm. The average of the first three experiments is 54.005 gm, of the fourth is 0.004 gm greater than the fifth, while the average of the sixth and seventh experiment was 0.010 gm less than the average of the first three. Find the weight of the body obtained by the fourth experiment.
One collective farm got an average harvest of 21 tons of wheat and another collective farm that had 12 acres of land less given to wheat, got 25 tons from a hectare. As a result, the second farm harvested 300 tons of wheat more than the first. How many tons of wheat did each farm harvest?
Read the following passage and answer the following question that follows.
Aman, Binod, Charan, Dharam and Ehsaan are the members of the same family. Each and everyone loves one another very much. Their birthdays are in different months and on different dates. Aman remembers that his birthday is between 25th and 30th, of Binod it is between 20th and 25th, of Charan it is between 10th and 20th, of Dharam it is between 5th and 10th and of Ehsaan it is between 1st and 5th of the month. The sum of the date of birth is defined as the addition of the date and the month, for example 12th January will be written as 12/1 and will add to a sum of the date of 13. (Between 25th and 30th includes 25 and 30).
If the dates of birth, of four of them are prime numbers, then find the maximum average of the sum of their dates of birth?
The average age of a group of persons going for a movie is 20 years. 10 new persons with an average age of 10 years join the group on the spot due to which the average of the group becomes 18 years. Find the number of persons initially going for the movie.
The average height of 22 toddlers increases by 2 inches when two of them leave this group. If the average height of these two toddlers is one-third the average height of the original 22, then the average height, in inches, of the remaining 20 toddlers is
The average of 30 integers is 5. Among these 30 integers, there are exactly 20 which do not exceed 5. What is the highest possible value of the average of these 20 integers?
Read the following:
There are 3 classes having 20, 25 and 30 students respectively having average marks in an examination as 20, 25 and 30 respectively. If the three classes are represented by A, B and C and you have the following information about the three classes,
answer the questions that follow:
A - Highest score 22, Lowest score 18
B - Highest score 31, Lowest score 23
C - Highest score 33, Lowest score 26
In a transfer of 5 students from B to C
Which of these can be said about the average score of B?
Three classes X, Y and Z take an algebra test.
The average score in class X is 83.
The average score in class Y is 76.
The average score in class Z is 85.
The average score of all students in classes X and Y together is 79.
The average score of all students in classes Y and Z together is 81.
What is the average for all the three classes?
Ten years ago, the ages of the members of a joint family of eight people added up to 231 years. Three years later, one member died at the age of 60 years and a child was born during the same year. After another three years, one more member died, again at 60, and a child was born during the same year. The current average age of this eight-member joint family is nearest to
|
191 videos|131 docs|110 tests
|
|
191 videos|131 docs|110 tests
|


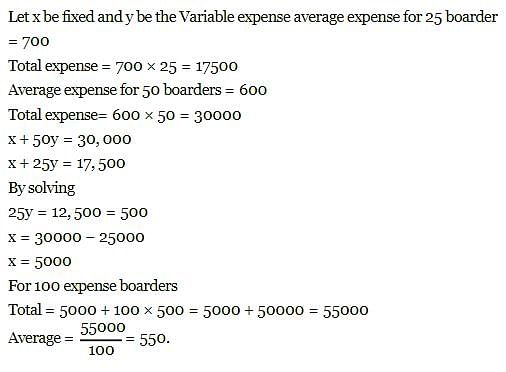

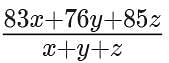
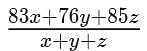 = (83*3/4 + 76 + 85*5/4)/(3/4 + 1 + 5/4) = 978/12 = 81.5
= (83*3/4 + 76 + 85*5/4)/(3/4 + 1 + 5/4) = 978/12 = 81.5









