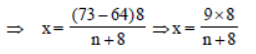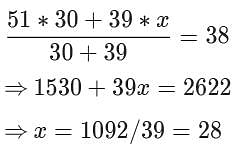Arun Sharma Test: Averages- 2 - CAT MCQ
15 Questions MCQ Test Quantitative Aptitude (Quant) - Arun Sharma Test: Averages- 2
The average weight of the books carried by Kuku to school is 1.5 kg and 2.5 kg is the average weight of the exercise books. If Kuku is carrying only text books and exercise books in the ratio of 3:4, what is the total weight of his school bag? (Ignore any other weights such as that of school bag, stationary etc.)
The average of eight numbers is 25, that of the first two is 20 and of the next three is 26. The sixth number is less than the seventh by 4, and less than the eighth by 6. The last number is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Three years ago , the average age of a family of 5 members was 17 years. Inspite of the birth of a child in the family, the present average age of the family remains the same. The present age of the child is
The average marks of a class of 48 students is 35. Of them, two score zero, of the rest, the first 30 scored an average of 40, the next fourteen scored an average of 20. If the remaining two scored equal marks, what are their individual marks?
The average mark of a class of n students is 64. When eight new students with an average mark of 73 join the class, the new average of the entire class is a whole number. Find the number of students now in the class, given that n lies between 25 and 60.
The average of 10 two-digit positive integers is Z. However, one number AB is taken as BA, then the average increases to Z + 2.7. What is the value of |B - A|?
The average rainfall for the first 3 days out of five days was recorded to be 0.45 inches. The rainfall on the last two days was in the ratio 2:3. The average of five days was 0.40 inches. What was the rainfall on the last day?
The average price of a share is the average of 5 readings taken at regular intervals in a day. The index price is taken by a weighted arithmetic average price of a class A and class B stock. The respective weights are 1.1 and 0.9 for the two kinds of stocks. If the five readings of a class A stock were 19, 26, 31, 35, 39 and for a class B stock the readings were 7, 8, 17, 20, 23 then what was the index price that day?
The average age of 24 students and the class teacher is 16 years. If the age of the class teacher is excluded the average reduces by 1 year. What is the age of the class teacher?
There are 20 students in Mr Rahul Ghosh’s class. He conducts an examination out of 100 and then arranged the marks in an ascending order. He found Chandan, the topper of the class, had slipped to the tenth position. When he was adding the scores of the last 11 students the average was 64 and that of the top 10 was 67. If the average marks obtained by all the students of his class was 65, how many marks did Chandan score?
The average marks of a student in 10 papers are 80. If the highest and the lowest scores are not considered, the average is 81. If his highest score is 92, find the lowest
Prof. Suman takes a number of quizzes for a course. All the quizzes are out of 100. A studentcan get an A grade in the course if the average of her scores is more than or equal to 90.Grade B isawarded to a student if the average of her scores is between 87 and 89 (both included). If the average isbelow 87, the student gets a C grade. Ramesh is preparing for the last quiz and he realizes that he willscore a minimum of 97 to get an A grade. After the quiz, he realizes that he will score 70, and he will justmanage a B. How many quizzes did Prof. Suman take?
The average of 7 consecutive numbers is P. If the next three numbers are also added, the average shall
In an apartment complex, the number of people aged 51 years and above is 30 and there are at most 39 people whose ages are below 51 years. The average age of all the people in the apartment complex is 38 years. What is the largest possible average age, in years, of the people whose ages are below 51 years?
Ramesh and Gautam are among 22 students who write an examination. Ramesh scores 82.5. The average score of the 21 students other than Gautam is 62. The average score of all the 22 students is one more than the average score of the 21 students other than Ramesh. The score of Gautam is
|
191 videos|131 docs|110 tests
|
|
191 videos|131 docs|110 tests
|