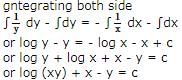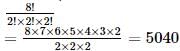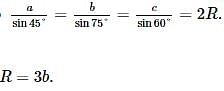BITSAT Maths Test - JEE MCQ
30 Questions MCQ Test BITSAT Mock Tests Series & Past Year Papers 2025 - BITSAT Maths Test
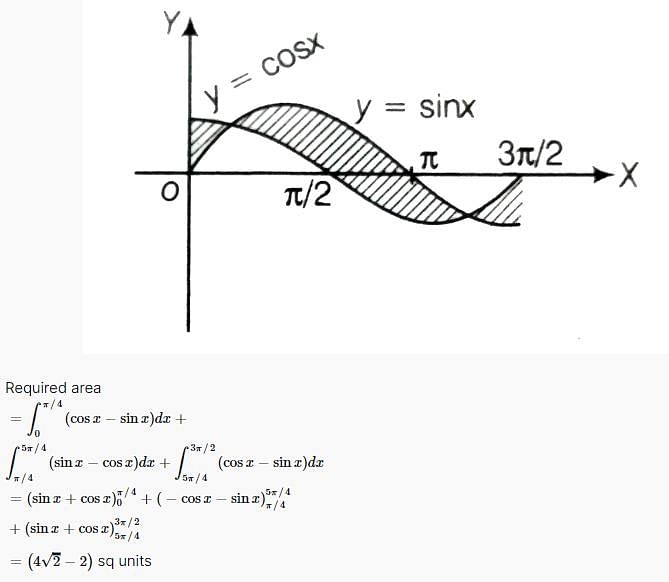
The area of the figure bounded by the curves y = cos x and y = sin x and the ordinates x = 0 and x = 3π/2 is
The sum of the coefficients in the expansion of (1+x-3x2)3148 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The equation of a circle which is ortho gonal to circles x2+y2+3x-5y+6=0 and 4x2+4y2-28x+29=0 and whose centre lies on the line 3x+4y+1=0 is
The equation of circle which passes through the points (3,-2) and (-2,0) and whose centre lies on the line 2x-y-3=0 is
The differential equation for the family of curves x2 + y2 - 2ay = 0, where a is an arbitrary constant is
From the top of a building of height h metres, the angle of depression of an object on the ground is α. The distance (in metres) of the object from the foot of the building is
The product of the perpendicular, drawn from any point on a hyperbola to its asymptotes is
The area of the region bounded by the curves y = |x-2|, x = 1, x = 3 and the x-axis is
The differential equation (d2y/dx2)2/3 = (y + (dy/dx))1/2 is of
The sum of first 50 terms of the series cot⁻1 3 + cot⁻1 7 + cot⁻1 13 + cot⁻1 21 + ... is
If B is a non-singular matrix and A is a square matrix, then det (B⁻1 AB) is equal to
If in a square matrix A=[aij], we find that
aij = aji ∀ i,j, then A is a
If the function f(x) = 2x3 - 9ax2 + 12a2x + 1, where a > 0, attains its max. and min. at p and q respectively such that p2 = q then a equals
The locus of the point of intersection of two normals to the parabola x2=8y, which are at right angles to each other,is
Each line represented by equation (x₁y-xy₁)2=a2(x2+y2) is at a distance from (x₁,y₁)
If the normal at the point t on a parabola y = 4ax meet it again at t1, then t1 =
The number of words formed from the letters of the word INDEPENDENCE when vowels are together is
The numbers of all words formed from the letters of the word CALCUTTA is
A problem in mathematics is given to 3 students whose chances of solving individually are 1/2, 1/3, and 1/4. The probability that the problem will be solved atleast by one is
The mean and variance of a Binomial distribution are 6 and 4. The parameter n is
In a ΔABC , A : B : C = 3 : 5 : 4 . Then a + b + c √2 is equal to
|
2 videos|17 docs|85 tests
|
|
2 videos|17 docs|85 tests
|