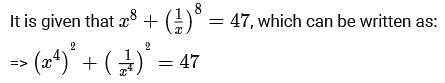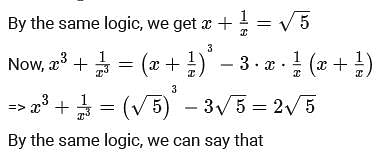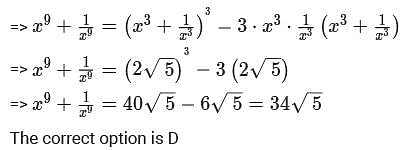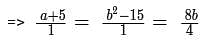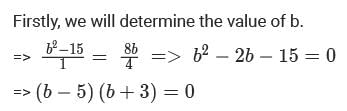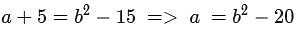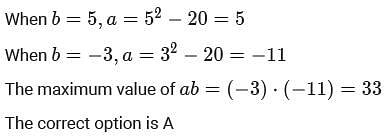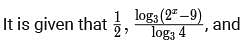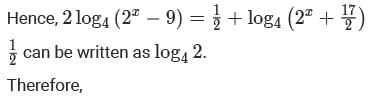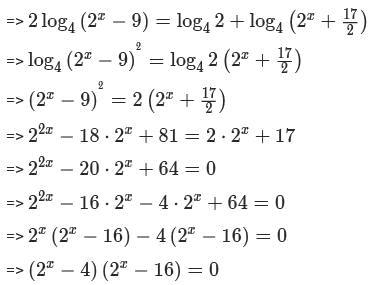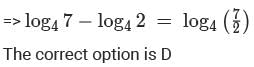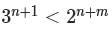CAT 2023 Slot 3 Question Paper (July 31) - CAT MCQ
15 Questions MCQ Test Daily Test for CAT Preparation - CAT 2023 Slot 3 Question Paper (July 31)
Which one of the following statements best expresses the paradox of patrimony laws?
It can be inferred from the passage that archaeological sites are considered important by some source countries because they:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which one of the following statements, if true, would undermine the central idea of the passage?
According to the author, for Pinker as well as the ancient Greek philosophers, rational thinking involves all of the following EXCEPT:
The author endorses Pinker’s views on the importance of logical reasoning as it:
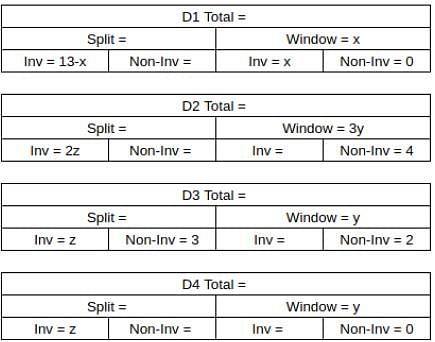
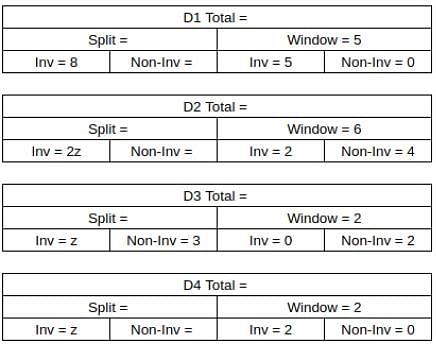
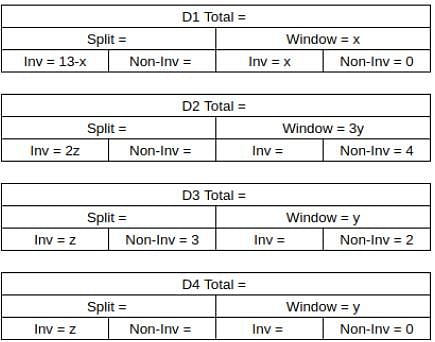
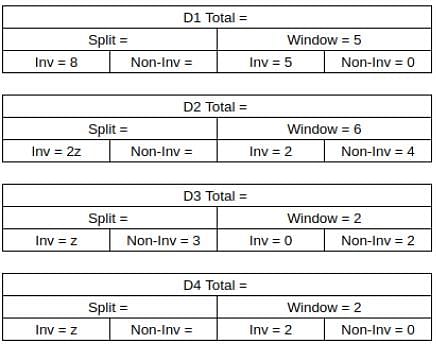
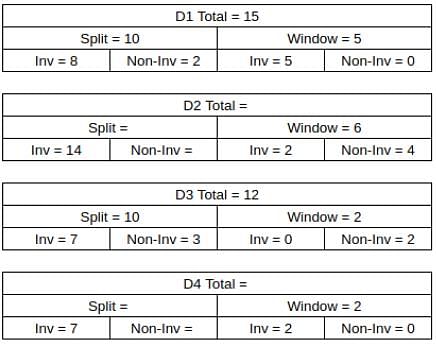
What percentage of ACs sold were of Non-inverter type?
What was the total number of ACs sold by D2 and D4?
Which of the following statements is necessarily false?
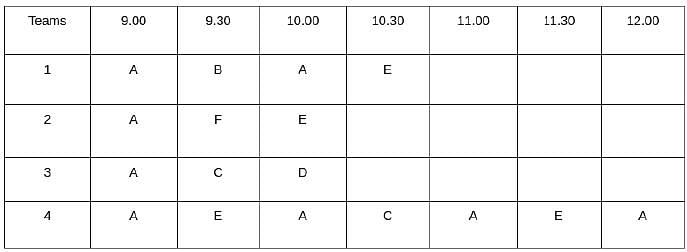
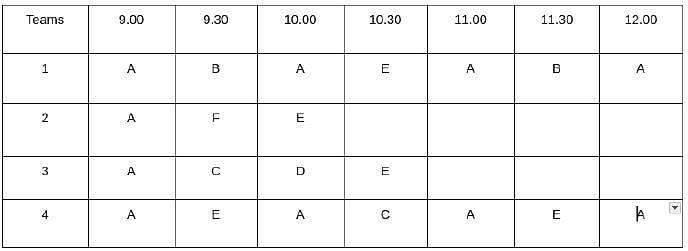
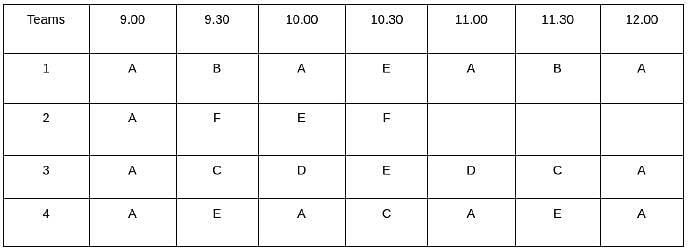
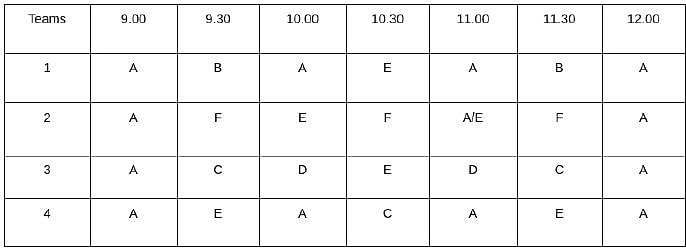
Which one among the following stations is visited the largest number of times?
If x is a positive real number such that 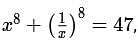 then the value of
then the value of 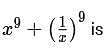
Let n and m be two positive integers such that there are exactly 41 integers greater than 8m and less than 8n, which can be expressed as powers of 2. Then, the smallest possible value of n + m is
For some real numbers a and b, the system of equations x+y = 4 and (a+5)x + (b2 -15)y = 8b has infinitely many solutions for x and y. Then, the maximum possible value of ab is
For a real number x, if 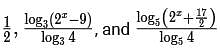 are in an arithmetic progression, then the common difference is
are in an arithmetic progression, then the common difference is
Let n be any natural number such that 5n-1 < 3n+1 . Then, the least integer value of m that satisfies 3n+1 < 2n+m for each such n, is
|
152 docs|327 tests
|