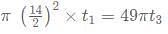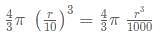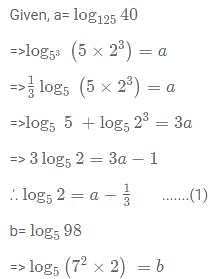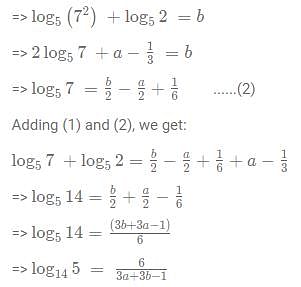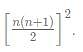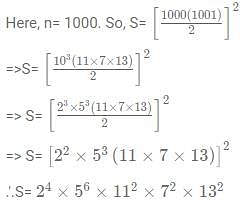CAT Mock Test- 3 (October 27) - CAT MCQ
30 Questions MCQ Test Daily Test for CAT Preparation - CAT Mock Test- 3 (October 27)
According to Charles Guignon, finding one's true self involves all of the following, EXCEPT:
The inner and performative modes of authenticity differ in all of the following ways, EXCEPT:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following statements is definitely TRUE according to the passage?
Which of the following statements CAN be inferred from the passage?
I. The tropical rain forest ecosystem would not have developed had the dinosaurs not gone extinct.
II. Location of the impact crater is crucial to understanding the effects of the meteoritic collision.
III. The effects of the collision on African tropical rain forests were not known until recently.
IV. Fires caused by the meteoritic collision led to the depletion of soil nutrients.
According to the passage, all of the following aided in the emergence of the Amazon rainforest ecosystem, EXCEPT:
DIRECTIONS for the question: The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
- Competition is the driving force behind the real benefits such systems achieve, but the logic of competition also imprisons its players to stay within their roles.
- Liberal democracy is like capitalism, a game designed to make its players compete against each other for points and prizes.
- As a result, democracies are surprisingly vulnerable to take over, as we have seen from the recent examples of Turkey, Hungary, and India.
- It is no one's job to defend the system of rules governing that competition.
DIRECTIONS for the question: The four sentences (labelled 1, 2, 3, 4) below, when properly sequenced, would yield a coherent paragraph. Decide on the proper sequencing of the order of the sentences and key in the sequence of the four numbers as your answer:
- By definition, parasites live in or on a host and take something from that host.
- Scientists warn of dire consequences if we disregard the rest.
- This has made them the pariahs of the animal world.
- But not all parasites cause noticeable harm to their hosts, and only a small percentage affect humans.
Direction: Choose the most logical order of sentences from among the given choices to construct a coherent paragraph.
1. This is only partially true because while most of the fighting did take place on the continent, one of the largest and most sophisticated undertakings of the war was conducted mainly at sea.
2. While the land war certainly contributed to the Entente's (Britain, France, Italy, U.S.) victory in 1918, it was the blockade that truly broke Germany's back.
3. This operation was the British blockade from 1914-1919 which sought to obstruct Germany's ability to import goods, and thus in the most literal sense starve the German people and military into submission.
4. The First World War is largely thought of as a conflict where the majority of the significant operations took place almost exclusively on mainland Europe with the exception of a handful of naval clashes fought throughout the world's oceans.
The passage given below is followed by four alternate summaries. Choose the option that best captures the essence of the passage.
Globalization promised an interconnected world, but it also led to significant parts of entire populations feeling left behind, stirring discontent and sociopolitical backlash. This unintended consequence has seen the rise of protectionism and nationalism, as those adversely affected seek to reclaim control over their economic prospects.
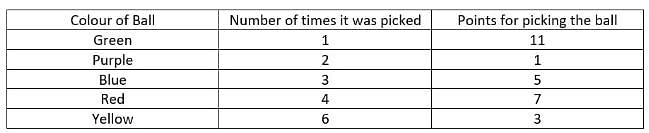
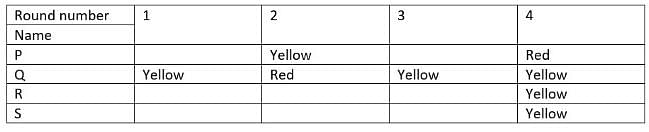
Winner is the person scoring the highest points at the end of all the rounds. Who is the winner?
How many more minimum conditions are required to find who picked what in all the rounds?
If points scored by R in round 3 were 5, what was the colour of the ball picked by S in round 1?
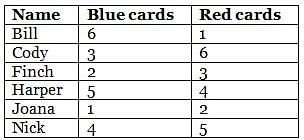
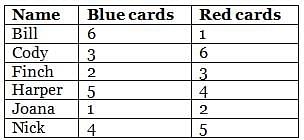
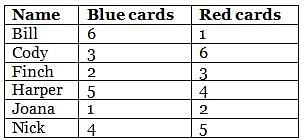
How many red cards more/less does Harper have than Bill? Key in the number.
If the third ranker voted for IIM-I, then the fifth ranker should have voted for
A cricket camp invited 500 cricket players who were batsmen, bowlers, and all-rounders(who can both bat and bowl). 60% of the players were batsman and 70% of them were bowlers. 50% of the pure batsmen (who can only bat), 60% of the pure bowlers (who can only bowl) and 20% of the all-rounders were left-handed. How many right-handed players were part of the cricket camp?
If x3 + 2x2−Ax has only one of its three real and unequal roots between [-1,3). Then the value of A can lie between?
A pizza store sold pizzas in 3 sizes- Small, medium and large with diameters of pizza equal to 8 inches, 11 inches and 14 inches. If the cost of the pizza depends on the volume of the pizza and the prices of the pizza are in the ratio 2:3:4, then the ratio of thickness of the small, medium and large pizza is in the ratio-
There is a dumbbell which consists of a solid long cylinder of radius r and height 10r with a solid hemisphere of radius 3r attached at either end as follows:
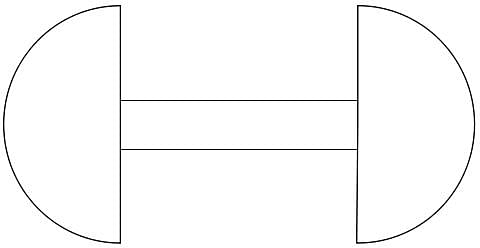
If this is molten and restructured into a maximum of N solid spheres of radius r/10, what is the value of N?
The values for which |(x-2)-|x+2||-5 ≥ 0 holds are:
What is the value of x for which 2(1+3+5+...x) = (0.0625)−25
If log125 40= a and log5 98 = b. Then how can log14 5 be represented in terms of a and b?
In how many ways can we select a square of side length at most 4 units from a chess board if one square of the chess board is considered to have a side length of 1 unit?
The number of even factors of S, where S = 13 + 23 + 33 +... 10003 is
What is the sum of the first 10 terms of an increasing A.P. where the first, second and fourth terms are in G.P. and the fifth term of the A.P. is 13?
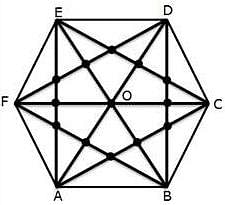
If all the diagonals of a regular hexagon are drawn, the number of points intersection, not counting the corners of the hexagon is
On the market of Covent Garden, Mrs. Smith and Mrs. Jones sell apples. Mrs. Jones sells her apples for two per rupee. The apples of Mrs. Smith are a bit smaller; she sells hers for three per rupee. At a certain moment, when both ladies have the same number of apples left, Mrs. Smith is being called away. She asks her neighbor to take care of her goods. To make everything not too complicated, Mrs. Jones simply puts all apples to one big pile, and starts selling them for two rupee per five apples. When Mrs. Smith returns the next day, all apples have been sold out. But when they start dividing the money, there appears to be a shortage of seven rupees. Supposing they divide the amount equally, how much in Rupees does Mrs. Jones lose in this deal?
|
152 docs|327 tests
|