CDS II - Mathematics Previous Year Question Paper 2017 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Previous Years Papers - CDS II - Mathematics Previous Year Question Paper 2017
A tent has been constructed which is in the form of a right circular cylinder surmounted by a right circular cone whose axis coincides with the axis of the cylinder. If the radius of the base is 50 m, the height of the cylinder is 10 m and the total height of the tent is 15 m, then what is the capacity of the tent in cubic meters?
Two rectangular sheets of sizes 2π × 4π and π × 5π are available. A hollow right circular cylinder can be formed by joining a pair of parallel sides of any sheets. What is the maximum possible volume of the cylinder that can be formed this way?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In triangle ABC, the medians AD and BE intersect at G. A line DF is drawn parallel to BE such that F is on AC. If AC = 9 cm, then what is CF equal to?

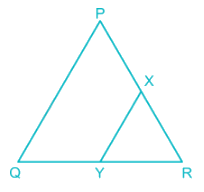
In a triangle PQR, X is a point on PR and Y is a point on QR such that PR = 10 cm, RX = 4 cm, YR = 2 cm, QR = 5 cm. Which one of the following is correct?
Consider the following statements in respect of three straight lines A, B and C on a plane:
1. If A and C are parallel and B and C are parallel, then A and B are parallel
2. If A is perpendicular to C and B is perpendicular to C, then A and B are parallel
3. If the acute angle between A and C is equal to the acute angle between B and C; then A and B are parallel
Q. Which of the above statements are correct?
The diagonals of a rhombus are of length 20 cm and 48 cm. What is the length of a side of the rhombus?
An arc of a circle subtends an angle π at the centre. If the length of the arc is 22 cm, then what is the radius of the circle?
(Take π = 22/7)
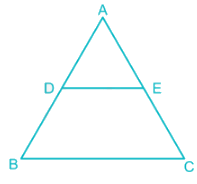
One fifth of the area of the triangle ABC is cut off by the line DE drawn parallel to BC such that D is on AB and E is one AC. If BC = 10 cm, then what is DE equal to?
There are 8 lines in a plane, no two of which are parallel. What is the maximum number of points at which they can intersect?
A closed polygon has six sides and one of its angles is 30° greater than each of the other five equal angles. What is the value of the equal angles?
Consider the following statements:
(1) The point of intersection of the perpendicular bisectors of the sides of a triangle may lie outside the triangle.
(2) The point of intersection of the perpendicular drawn from the vertices to the opposite side of a triangle may lie on two sides.
Q. Which of the above statements is/are correct?
Directions: In a University, there are 1200 students studying four different subjects, Mathematics, Statistics, Physics and Chemistry. 20% of the total number of students are studying Mathematics, one-fourth of the total number of students are studying Physics, 320 students are studying Statistics. Three-fifth of the total number of students studying Chemistry are girls. 150 boys are studying Mathematics. 60% of the students studying Physics are boys. 250 girls are studying Statistics.
Q. What is the total number of boys studying Statistics and Physics?
Directions: In a University, there are 1200 students studying four different subjects, Mathematics, Statistics, Physics and Chemistry. 20% of the total number of students are studying Mathematics, one-fourth of the total number of students are studying Physics, 320 students are studying Statistics. Three-fifth of the total number of students studying Chemistry are girls. 150 boys are studying Mathematics. 60% of the students studying Physics are boys. 250 girls are studying Statistics.
Q. The number of girls studying Statistics is what percent (approximate) of the total number of students studying Chemistry?
Directions: In a University, there are 1200 students studying four different subjects, Mathematics, Statistics, Physics and Chemistry. 20% of the total number of students are studying Mathematics, one-fourth of the total number of students are studying Physics, 320 students are studying Statistics. Three-fifth of the total number of students studying Chemistry are girls. 150 boys are studying Mathematics. 60% of the students studying Physics are boys. 250 girls are studying Statistics.
Q. In which subjects is the difference between the number of boys and girls is equal?
Directions: In a University, there are 1200 students studying four different subjects, Mathematics, Statistics, Physics and Chemistry. 20% of the total number of students are studying Mathematics, one-fourth of the total number of students are studying Physics, 320 students are studying Statistics. Three-fifth of the total number of students studying Chemistry are girls. 150 boys are studying Mathematics. 60% of the students studying Physics are boys. 250 girls are studying Statistics.
Q. What is the difference between number of boys studying in Mathematics and number of girls studying in Physics?
Directions: In a University, there are 1200 students studying four different subjects, Mathematics, Statistics, Physics and Chemistry. 20% of the total number of students are studying Mathematics, one-fourth of the total number of students are studying Physics, 320 students are studying Statistics. Three-fifth of the total number of students studying Chemistry are girls. 150 boys are studying Mathematics. 60% of the students studying Physics are boys. 250 girls are studying Statistics.
Q. What is the ratio between total number of boys to the total number of girls?
Frequency density of a class is computed by the ratio
A small company pays each of its 5 category ‘C’ workers Rs. 20,000, each of its 3 category ‘B’ workers Rs. 25,000 and a category ‘A’ worker Rs. 65,000. The number of workers earning less than the mean salary is
A man travelled 12 km at a speed of 4 km/h and further 10 km at a speed of 5 km/hr. What was his average speed?
The pie diagrams on the monthly expenditure of two families A and B are drawn with radii of two circles taken in the ratio 16 : 9 to compare their expenditures.
Q. Which one of the following is the appropriate data used for the above mentioned pie diagram?
Consider the following statements:
Statement I: The value of a random variable having the highest frequency is mode
Statement II: Mode is unique
Q. Which one of the following is correct in respect to the above statements?
Which one of the following is not correct?
The proportion of various items in a pie diagram is proportional to the
The geometric mean of x and y is 6 and the geometric mean of x, y and z is also 6. Then the value of z is
The total number of live births in a specific locality during different months of a specific year was obtained from the office of the Birth registrar. This set of data may be called
The heights (in cm) of 5 students are 150, 165, 161, 144 and 155. What are the values of mean and median (in cm) respectively?
The average height of 22 students of a class is 140 cm and the average height of 28 students of another class is 152 cm. What is the average height of students of both classes?
To maintain 8 cows for 60 days, a milkman spends Rs. 6400. To maintain 5 cows for n days, he spends Rs. 4800. What is the value of n?
A student secure 40% of the marks to pass an examination. He gets only 45 marks and fails by 5 marks. The maximum marks are
What is the value of u in the system of equations 3 (2u + v) = 7uv, 3 (u + 3v) = 11uv?
Five years ago, Ram was three times as old as Shyam. Four years from now, Ram will be only twice as old as Shyam. What is the present age of Ram?
|
56 docs|18 tests
|
|
56 docs|18 tests
|