CSIR NET Mathematics Mock Test - 2 - CSIR NET Mathematics MCQ
30 Questions MCQ Test CSIR NET Mathematics Mock Test Series - CSIR NET Mathematics Mock Test - 2
A number, when divided by 221, leaves a remainder 64. What is the remainder if the same number is divided by 13?
The first step to getting output from a laser is to excite an active medium. What is this process called?
Arrange the following steps of teaching in a logical order.
(i) Diagnosis of the learner
(ii) Fixing goals and content
(iii) Actions and Reactions
(iv) Feedback to teaching
(v) Decision about the strategy
(vi) Appropriate testing devices
Code:
In which decade with the first transatlantic radio broadcast occur?
In which decade was the first solid state integrated circuit demonstrated?
Pointing to a girl Priyankesh said,” She is the only daughter of the father of my sister’s brother”. How is she related to Priyankesh ?
Anjali says, He is the only son of the father of my sister's brother. How is that person related to Anjali?
Three numbers are such that first number is 15% of third number and second number is 25% of third number. Find the product of numbers if the sum of three numbers is 14.
Two points A and B on the surface of the Earth have the following latitude and longitude co-ordinates-
30°N, 45°E
30°N, 135°W
If R is the radius of the Earth, the length of the shortest path from A to B is-
(A) 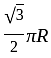 (B)
(B) 
(C) 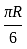 (D)
(D) 
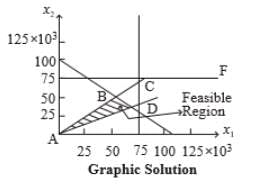
Maximize Z = 0·1x1 + 0·2x2
Subject to the constraints
x1 + x2 ≤ 1,00,000
x1 ≤ 75,000
x2 ≤ 75,000
0·1x1 + 0·2x2 ≥ 0·12(x1 + x2)
The number of words that can be formed by permuting the letters of ‘MATHEMATICS’ is
Let 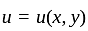 be the complete integral of the
be the complete integral of the 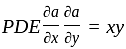 passing through the points (0, 0, 1) and
passing through the points (0, 0, 1) and 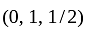 in the x-y-u space. Then the value of
in the x-y-u space. Then the value of 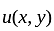 evaluated at (-1, 1)
evaluated at (-1, 1)
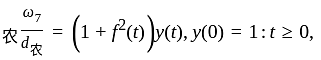 where
where 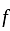 is a bounded continuous function on
is a bounded continuous function on 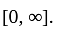 Then
Then
The solution of the Cauchy problem for the first order PDE  on
on 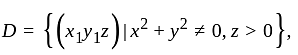 , with the initial condition
, with the initial condition 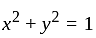 is
is
If 1, ω, ω2 are the cube roots of unity, then roots of (x - 1)3 + 8 = 0 are –
If A and B are idempotent matrix, then AB is idempotent, if—
If in a matrix A, two columns are interchanged and we obtain matrix B, then—
Consider the following statements:
I. A function f : z → z, defined by f(x) = x + 1, is one-one as well as onto.
II. A function f: N → N, defined by f(x) = x + 1, is one-one but not onto.
Which of the above statements is/are correct?
Consider the functional
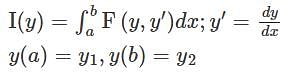
where 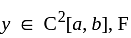 has second order continuous partial derivatives with respect to
has second order continuous partial derivatives with respect to 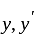 and
and 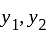 are given real numbers. Let
are given real numbers. Let 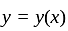 be an extremizing function for the functional
be an extremizing function for the functional
I. Then, along the extremizing curve-













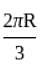
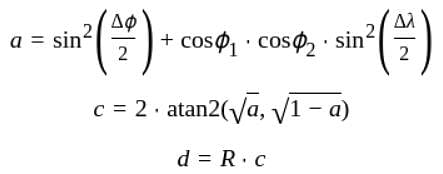

 satisfies the PDE
satisfies the PDE
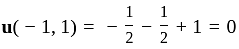
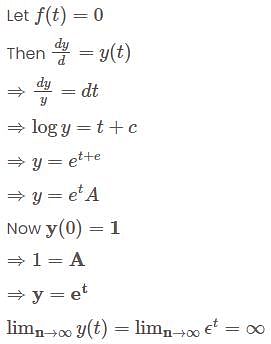

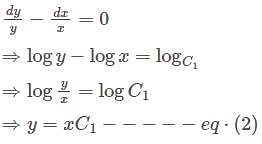
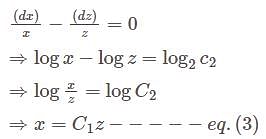

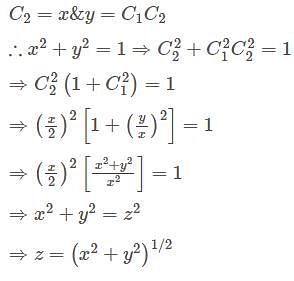
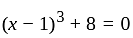


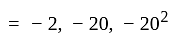
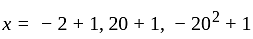
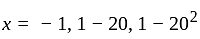
 when
when  is
is





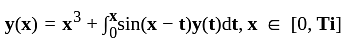
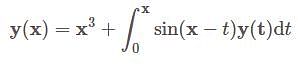
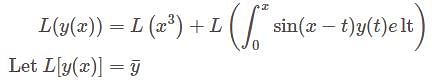
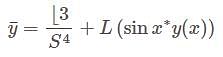
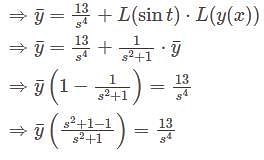
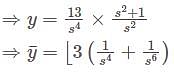
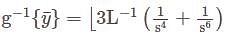

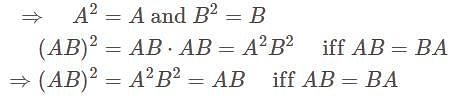
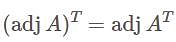
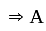 is Symmetric if
is Symmetric if 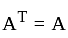
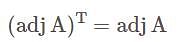
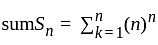
 The series is divergent series.
The series is divergent series.
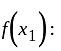

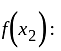
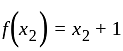
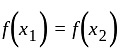
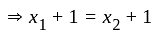
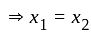
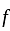 is one-one function.
is one-one function.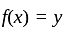

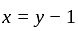
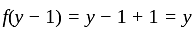
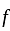 is onto.
is onto.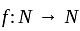 , define
, define 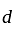 by
by 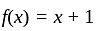 , is one-one but not onto.
, is one-one but not onto.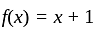 ,
,
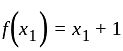
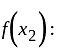
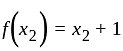
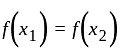
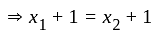
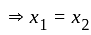
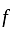 is one-one function.
is one-one function.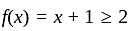 for all
for all 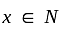
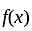 does not assume values
does not assume values 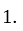
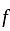 is not an onto function.
is not an onto function.















 is a solution of the integral equation.
is a solution of the integral equation.
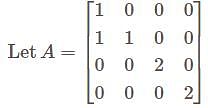


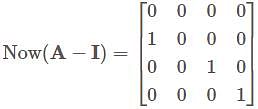
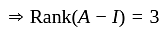
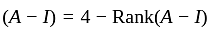

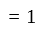
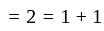
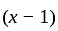 in minimal polynomial
in minimal polynomial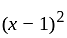 is factor of minimal polynomial
is factor of minimal polynomial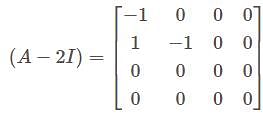

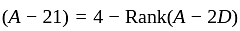
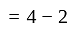

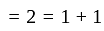 and G.M. of 1 is 1.
and G.M. of 1 is 1.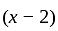 in minimal polynomial So
in minimal polynomial So  is factor of minimal polynomial
is factor of minimal polynomial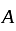 is
is 
 is said to be Hermitian if
is said to be Hermitian if  for all
for all  .
. to be a Hermitian is that
to be a Hermitian is that 
 is a hermitian matrix.
is a hermitian matrix. then power set of A is
then power set of A is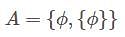


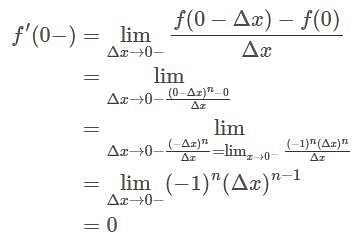
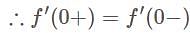
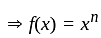 is differentiable at x = 0
is differentiable at x = 0














