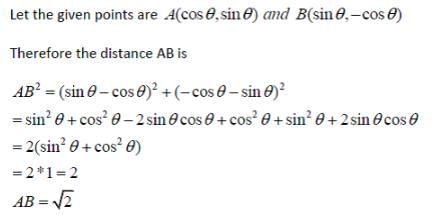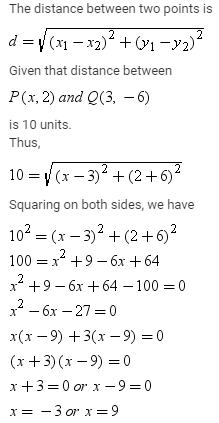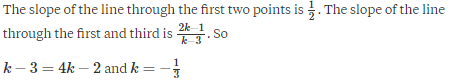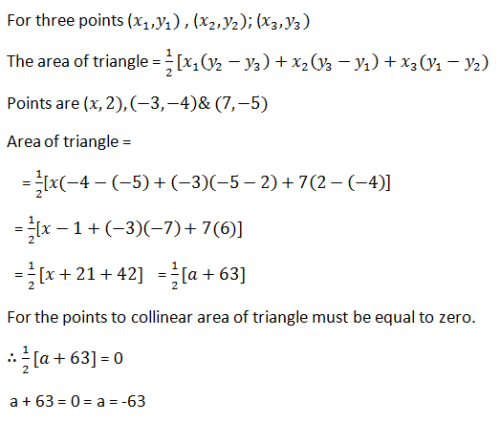Coordinate Geometry - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ
25 Questions MCQ Test - Coordinate Geometry - Olympiad Level MCQ, Class 9 Mathematics
The distance between the points (cos θ, sin θ) and (sin θ, – cos θ) is:
The distance between the points (a cos 35°, 0) and (0, a cos 65°) is :
If x is a positive integer such that the distance between points P(x, 2) and Q(3, –6) is 10 units, then x =
The distance between the points (a cos θ + b sin θ, 0) and (0, a sin θ – b cos θ) is :
If the distance between the points (4, p) and (1, 0) is 5, then p =
A line segment is of length 10 units. If the coordinates of its one end are (2, –3) and the abscissa of the other end is 10, then its ordinate is :
The perimeter of the triangle formed by the points (0, 0), (1, 0) and (0, 1) is :-
If A(2, 2), B(–4, –4) and C(5, –8) are the vertices of a triangle, then the length of the median through vertex C is :
If three points (0, 0), (3, 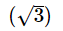 and (3, λ) form an equilateral triangle, then λ =
and (3, λ) form an equilateral triangle, then λ =
If the points (k, 2k), (3k, 3k) and (3, 1) are collinear, then k :
The coordinate of the point on X-axis which are equidistant from the points (–3, 4) and (2, 5) are :
If A(5, 3), B(11, –5) and P(12, y) are the vertices of a right triangle right angled at P, then y =
The area of the triangle formed by (a, b + c), (b, c + a) and (c, a + b) is :
If (x – 2), (–3, –4) and (7, –5) are collinear, then x =
If points (t, 2t), (–2, 6) and (3, 1) are collinear, then t =
If the area of the triangle formed by the points (x, 2x), (–2, 6) and (3, 1) is 5 square units, then x =
The line segment joining points (–3, –4), and (1, –2) is divided by y-axis in the ratio :
The ratio in which (4, 5) divides the join of (2, 3) and (7, 8) is :
The ratio in which the x-axis divides the segment joining (3, 6) and (12, –3) is :
If points (1, 2), (–5, 6) and (a, –2) are collinear, then a =
The point A(3, 4) lies in
The point B(-3, 4) lies in
The point C(-5, -2) lies in
The point D(3, -6) lies in
The point P(3, 0) lies