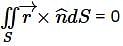GATE Mathematics Mock Test - 3 - GATE Mathematics MCQ
30 Questions MCQ Test GATE Mathematics Mock Tests - GATE Mathematics Mock Test - 3
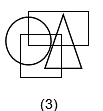
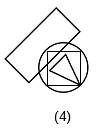
Directions: In the following question, from amongst the figures marked (1), (2), (3) and (4), select the one which satisfies the same conditions of placement of the dots as in figure (X)
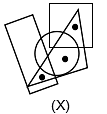
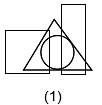
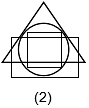





Which of the following is an antonym of the word PROFESSIONAL?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
While cutting, if the plane is at an angle and it cuts all the generators, then the conic formed is called as ______
For the function f(x) = x2 – 2x + 1
we have Rolles point at x = 1. The coordinate axes are then rotated by 45 degrees in anticlockwise sense. What is the position of new Rolles point with respect to the transformed coordinate axes
For the infinitely defined discontinuous function

How many points 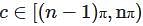 such that
such that
The sections cut by a plane on a right circular cone are called as ______
For the function f(x) = x3 + x + 1
we do not have any Rolles point. The coordinate axes are transformed by rotating them by 60 degrees in anti-clockwise sense. The new Rolles point is
It is suitable to use Binomial Distribution only for
If y = 3e2x + e-2x - αx is the solution of the initial value problem 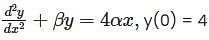 and
and 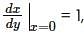 , where
, where 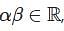 then α + β is (Answer should be integer) ________.
then α + β is (Answer should be integer) ________.
The smallest order for a group to have a non-abelian proper sub-group is (Answer should be integer) _________.
Consider the vector field 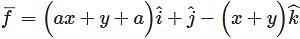 , where 'a' is a constant. If
, where 'a' is a constant. If 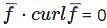 then the value of 'a' is (Answer should be integer)________.
then the value of 'a' is (Answer should be integer)________.
Let a be an element in a group G. If 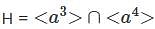 is a cyclic subgroup of <a> and H = <ak>. Then k is ________.
is a cyclic subgroup of <a> and H = <ak>. Then k is ________.
Value of the 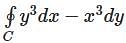 (where C are the two circles of radius 2 and 1 centered at the origin with positive orientation.)
(where C are the two circles of radius 2 and 1 centered at the origin with positive orientation.)
Let V be the vector space of real polynomials of degree atmost 2. which defines a linear operator 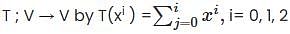 then the matrix of T–1 with respect to the basis (1, x, x2 ) is
then the matrix of T–1 with respect to the basis (1, x, x2 ) is
Let T: R2→ R3 be the Linear transformation whose matrix with respect to standard basis of R3 and R2 is  The T
The T
Suppose f ; ℝ→ℝ is an odd and differentiable fraction. Then for every x0 ∈ ℝ. f'(-x0) is equal to;
Let L(x) be the linearization of f(x) = sin x + 1 at the point x = π . Find L(π / 2).
Let h be a continuous and differentiable function defined on [0, 2π]. Some function values of h and h’ are given by the chart below:
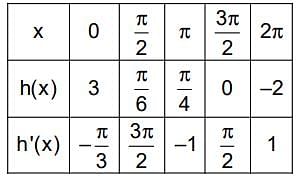
If p(x) = sin2(h(2x)),then p’ (π / 2) is not equal to ____
If 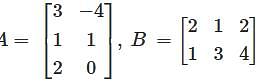 then which of the following statements are false ?
then which of the following statements are false ?
Let f: ℝ2 →ℝ and g :ℝ2 →ℝ be defined by f(x,y) = |x| + |y| and g(x,y) = |xy|. Then,
The number of elements of order 15 in the group S1 is (Answer should be integer) ________.
Evaluate 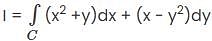 from A = (0, 2) to B = (3, 5) along the curve y = 2 + x is (Answer should be integer) _________.
from A = (0, 2) to B = (3, 5) along the curve y = 2 + x is (Answer should be integer) _________.
Let V be the volume enclosed by a piecewise smooth closed surface S. Then  is equal to (Answer should be integer) _____________.
is equal to (Answer should be integer) _____________.


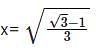
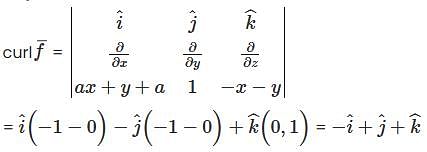
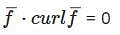
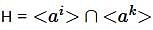 is cyclic subgroup of <a> and
is cyclic subgroup of <a> and 
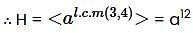
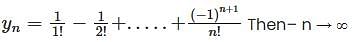
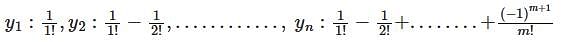
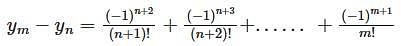
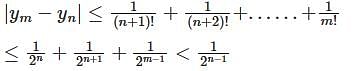
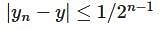
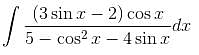
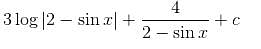
 and if
and if 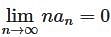 then
then 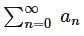 is
is 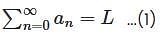
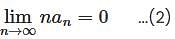
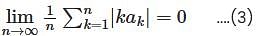
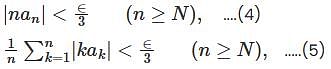
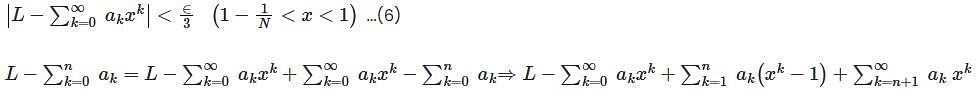
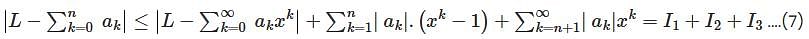
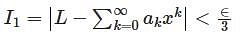
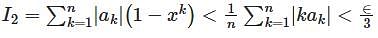
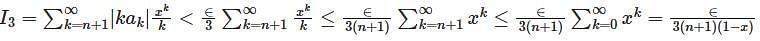
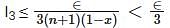

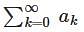 converges to L.
converges to L.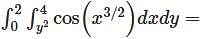


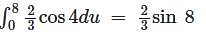
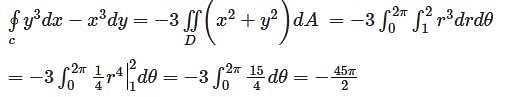
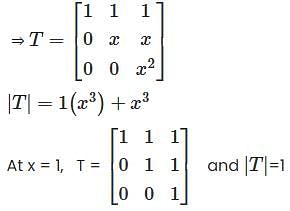
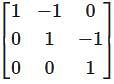


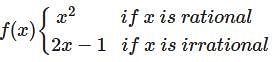 then,
then,
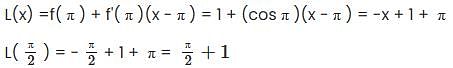
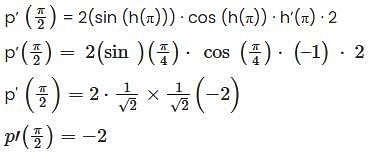
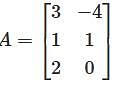
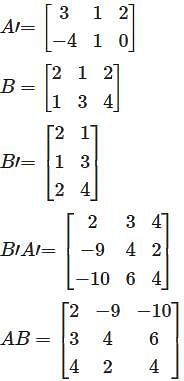
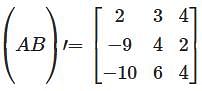
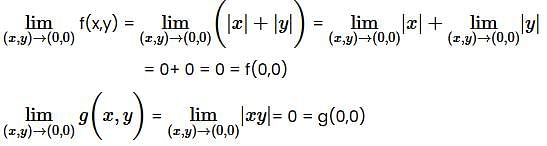
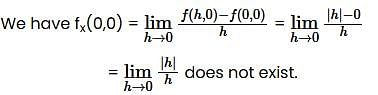
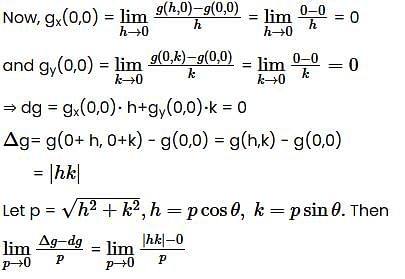
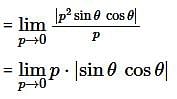
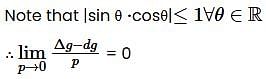
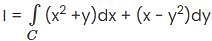
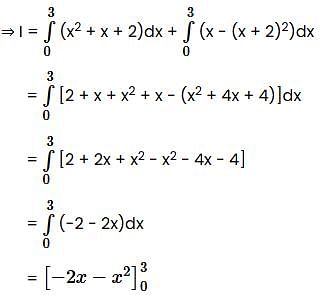
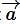 be an arbitrary constant vector Then,
be an arbitrary constant vector Then,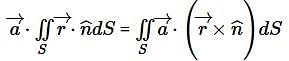
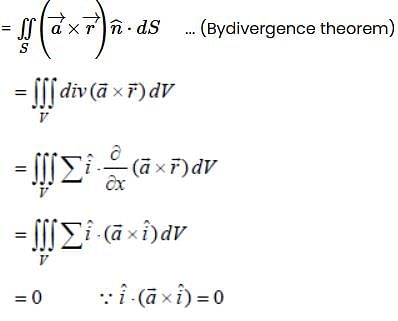
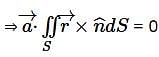 for any arbitrary constant vector
for any arbitrary constant vector 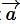 .
.