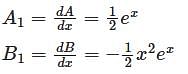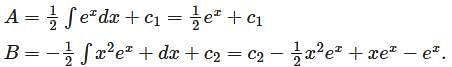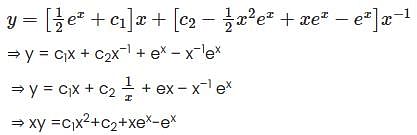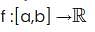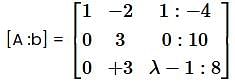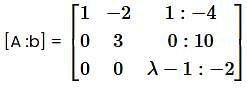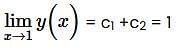GATE Mathematics Mock Test - 4 - GATE Mathematics MCQ
30 Questions MCQ Test GATE Mathematics Mock Tests - GATE Mathematics Mock Test - 4
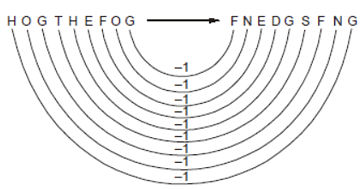
If HOG THE FOG → FNE DGS FNG, CPN FIU QPN → MOP THE MOB Then SOB THE BOSS
The number lock of a suitcase has 4 wheels, each labelled with ten digits, i.e. from 0 to 9. The lock opens with a sequence of four digits with no repeats. What is the probability of a person getting the sequence to open the suitcase?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Fill in the blank with the correct
The police were unable to the crowd.
Directions: In the question given below, a statement is followed by three courses of action labelled (A), (B) and (C). A course of action is a step or administrative decision to be taken for improvement, follow-up or further action in regard to the problem, policy, etc. On the basis of the information given in the statement, you have to assume everything in the statement to be true and then decide which of the suggested courses of action logically follow(s) for pursuing.
Statement: Many political activists have decided to stage demonstrations and block traffic movement in the city during peak hours to protest against the steep rise in prices of essential commodities.
Courses of action:
(A) The Govt. should immediately ban all forms of agitations in the country.
(B) The police authority of the city should deploy additional forces all over the city to help traffic movement in the city.
(C) The state administration should carry out preventive arrests of the known criminals staying in the city.
In a class, 40% of the students enrolled for Math and 70% enrolled for Economics. If 15% of the students enrolled for both Math and Economics, what % of the students of the class did not enroll for either of the two subjects?
The following question has four statements of three segments each. Choose the alternative where the third segment in the statement can be deduced using both the preceding two but not just from one of them.
A. Sonia is an actress. Some actresses are pretty. Sonia is pretty.
B. All actors are pretty. Manoj is not an actor. Manoj is not pretty
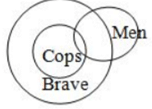
C. Some men are cops. Some men are brave. Some brave people are cops.
D. All cops are brave. Some men are cops. Some men are brave.
The collection may improve only if the govemment raises taxes.
Whenever the taxes are raised, the collections improve.
The collections never improve when taxes are raised.
The collections will not improve if the taxes are not raised.
Which of the following can be logically inferred from the above statement?
Let T : R3 → R3 be the linear transformation such that Y(1, 0, 1) = (0, 1 , –1) and T(2, 1, 1)= (3, 2, 1) Then T(–1, –2, 1)
Let S be a closed surface and let denote the position vector of any point (x,y,z) measured from an origin O. then 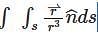 is equal to (if O lies inside S).
is equal to (if O lies inside S).
Let A be an n-by-n matrix with coefficients in F, having rows{a1, ..., an). Then which one of the statement is true for the matrix A?
The function f : ℝ ℝ → satisfied 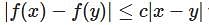 for all x, y ∈ and some constant c ∈ Then,
for all x, y ∈ and some constant c ∈ Then,
Consider the differential equation 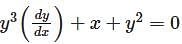 which of the following statements is true ?
which of the following statements is true ?
Let S3 be the group of all permutation with 3 symbols then the number of elements in S3 that satisfy the equation x2 = e (where e is identity) is (Answer should be integer) __________.
Number of homomorphism from ℤ8 ⊕ ℤ2, onto ℤ4 ⊕ ℤ4, (Answer Should be integer) _______.
If R→R is given by f(x) = x3 + x2f'(1) + xf''(2) + f'''(3) for all x in R. then f(2) - f(1) is
The orthogonal trajectories of the family of curves y = c1x3, where c1 is arbitary costant, is
Let  denote the eigenvalues of the matrix
denote the eigenvalues of the matrix 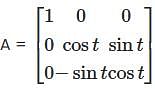
If 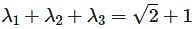 , then the set of possible values of t, -π ≤ t < π, is
, then the set of possible values of t, -π ≤ t < π, is
Which of the following are the wrong basis of the subspace spanned by the vectors α1= (1, 2, 3), α2 = (2, 1, –1),α3 = (1, –1, –4), α4 = (4, 2, –2)?
Apply the method of variation of parameters to solve x2 y2 + xy1 – y = x2 ex then
Let f: [a, b] → ℝ. Which of the following statement is/are true?
Let A ≠ 1,A ≠ 0 be a 3 x 3 real matrix such that A2 = A. Then which of the following statement are true?
Given 2x - y+2z = 2, x - 2y + z = -4 and x + y + λz = 4, then the value of λ such that the given system of equation has no solution is (Answer should be integer) ____________.
Let y(x) be the solution of x2y" - 2xy' - 4y = 0, y (1) =1. Then 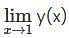 is _________
is _________


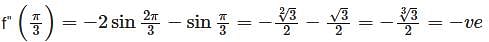
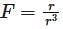 has a point to discontinuity at the origin. To remove this difficulty, let us enclose the origin by a small sphare Σ of radius ε.
has a point to discontinuity at the origin. To remove this difficulty, let us enclose the origin by a small sphare Σ of radius ε. 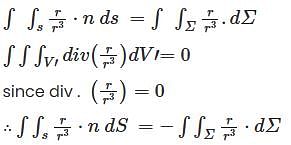
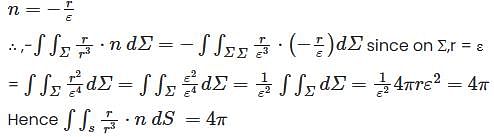

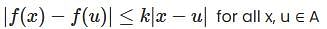
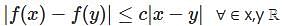
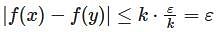
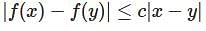

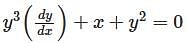
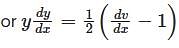
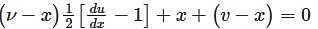

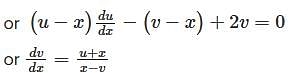
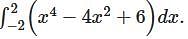
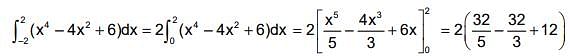
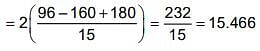
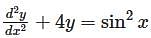 is given by ,
is given by , 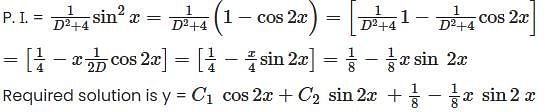
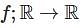
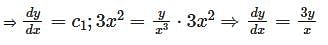
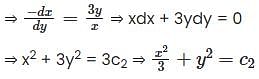
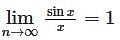 here f is continuous over [0, 1], so f(x) is uniformly continuous.
here f is continuous over [0, 1], so f(x) is uniformly continuous.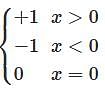
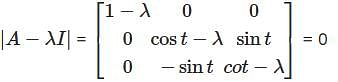
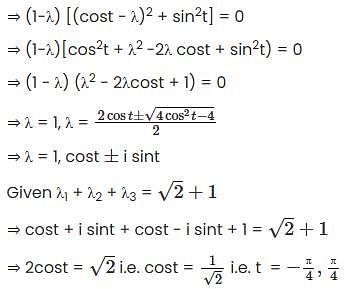
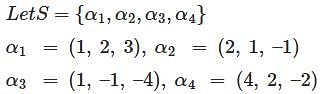
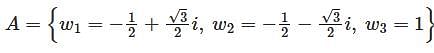 the cube roots do not form.
the cube roots do not form. 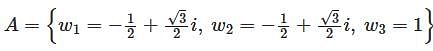
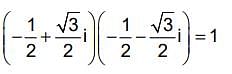
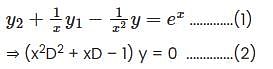
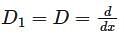 then eq (2) become
then eq (2) become