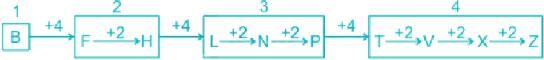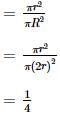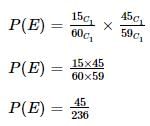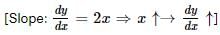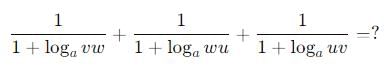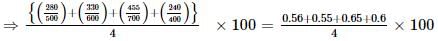General Aptitude - 3 - GATE Chemistry MCQ
20 Questions MCQ Test GATE Chemistry Mock Test Series - General Aptitude - 3
The number of Hens, Ducks, and Goats in farm P are 65, 91 and 169, respectively. The total number of Hens, Ducks and Goats in a nearby farm Q is 416. The ratio of hens : ducks : goats in farm Q is 5 : 14 : 13. All the hens, ducks and goats are sent from farm Q to farm P.
The new ratio of hens : ducks : goats in farm P is ____________.
Find the missing sequence in the letter series.
B, FH, LNP, __________.
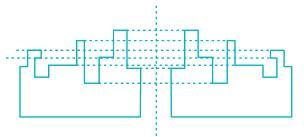
A jigsaw puzzle has 2 pieces. One of the pieces is shown above. Which one of the given options for the missing piece when assembled will form a rectangle? The piece can be moved, rotated or flipped to assemble with the below piece.


If 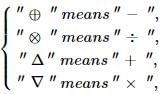
then, the value of the expression Δ 2 ⊕ 3 Δ ((4 ⊗ 2) ∇ 4) =
The distribution of employees at the rank of executives, across different companies C1, C2, ..., C6 is presented in the chart given above. The ratio of executives with a management degree to those without a management degree in each of these companies is provided in the table above. The total number of executives across all companies is 10,000.
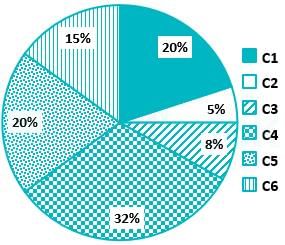
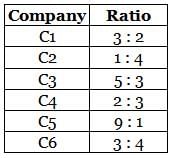
Q. The total number of management degree holders among the executives in companies C2 and C5 together is _____.
A digital watch X beeps every 30 seconds while watch Y beeps every 32 seconds.They beeped together at 10 AM.The immediate next time that they will beep together is _____.
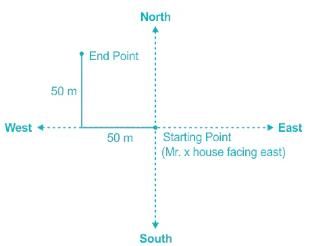
The front door of Mr X's house faces East. Mr X leaves the house, walking 50 m straight from the back door that is situated directly opposite to the front door. He then turns to his right, walks for another 50 m and stops. The direction of the point Mr X is now located at with respect to the starting point is ______.
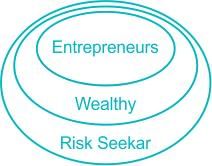
Given below are two statements 1 and 2, and two conclusions I and II.
Statement 1: All entrepreneurs are wealthy.
Statement 2: All wealthy are risk seekers.
Conclusion I: All risk seekers are wealthy.
Conclusion II: Only some entrepreneurs are risk seekers.
Based on the above statements and conclusions, which one of the following options is CORRECT?
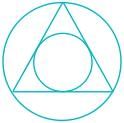
The ratio of the area of the inscribed circle to the area of the circumscribed circle of an equilateral triangle is _____
A box contains 15 blue balls and 45 black balls. If 2 balls are selected randomly, without replacement, the probability of an outcome in which the first selected is a blue ball and the second selected is a black ball, is ______.
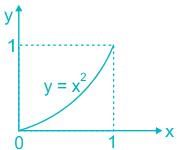
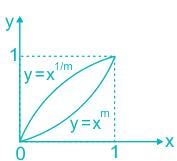
Select the graph that schematically represents BOTH y = xm and y = x1/m properly in the interval 0 ≤ x ≤ 1, for integer values of m, where m > 1.
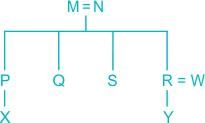
M and N had four children P, Q, R and S. Of them, only P and R were married. They had children X and Y respectively. If Y is a legitimate child of W, which one of the following statements is necessarily FALSE?
Given that a and b are integers and a + a2 b3 is odd, which one of the following statements is correct?
A person divided an amount of Rs. 100,000 into two parts and invested in two different schemes. In one he got 10% profit and in the other he got 12%. If the profit percentages are interchanged with these investments he would have got Rs.120 less. Find the ratio between his investments in the two schemes.
Consider the following three statements:
(i) Some roses are red.
(ii) All red flowers fade quickly.
(iii) Some roses fade quickly.
Q. Which of the following statements can be logically inferred from the above statements?
A rectangle becomes a square when its length and breadth are reduced by 10 m and 5 m, respectively. During this process, the rectangle loses 650 m2 of area. What is the area of the original rectangle in square meters?
It was estimated that 52 men can complete a strip in a newly constructed highway connecting cities P and Q in 10 days. Due to an emergency, 12 men were sent to another project. How many numbers of days, more than the original estimate, will be required to complete the strip?
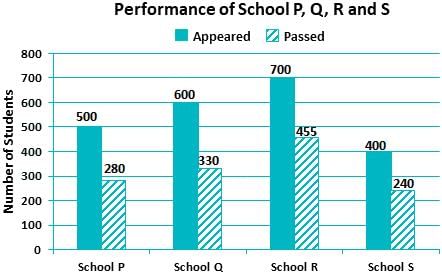
The bar graph shows the data of the students who appeared and passed in an examination for four school P, Q, R and S. The average of success rates (in percentage) of these four schools is _____.
What is the least multiple of 7, which when divided by 2, 3, 4, 5 and 6, leaves the remainders 1, 2, 3, 4, 5 respectively?
|
20 docs|37 tests
|