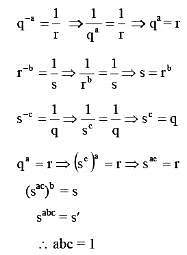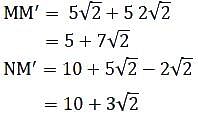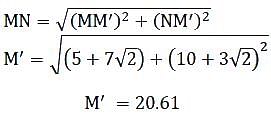General Aptitude - 5 - GATE Chemistry MCQ
20 Questions MCQ Test GATE Chemistry Mock Test Series - General Aptitude - 5
40% of deaths on city roads may be attributed to drunken driving. The number of degree needed to represent this as a slice of a pie chart is
Fatima starts from point P, goes North for 3 km, and then East for 4km to reach point Q. She then turns to face point P and goes 15km in that direction. She then goes North for 6km. How far is she from point P, and in which direction should she go to reach point P?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
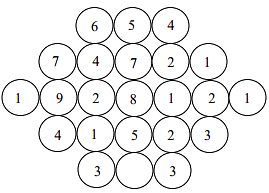
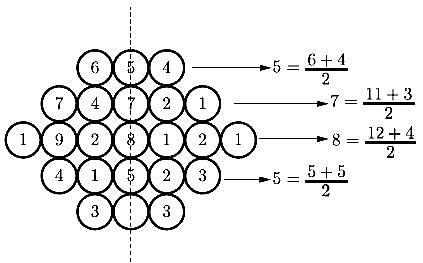
The number of 3-digit numbers such that the digit 1 is never to the immediate right of 2 is
A person moving through a tuberculosis prone zone has a 50% probability of becoming infected.However, only 30% of infected people develop the disease. What percentage of people moving through a tuberculosis prone zone remains infected but does not show symptoms of disease?
P, Q, R and S are working on a project. Q can finish the task in 25 days, working alone for 12hours a day. R can finish the task in 50 days, working alone for 12 hours per day. Q worked 12 hours a day but took sick leave in the beginning for two days. R worked 18 hours a day on all days. What is the ratio of work done by Q and R after 7 days from the start of the project?
A rule states that in order to drink beer one must be over 18 years old. In a bar, there are 4 people. P is 16 years old, Q is 25 years old, R is drinking milkshake and S is drinking beer. What must be checked to ensure that the rule is being followed ?
500 students are taking one or more courses out of Chemistry, Physics, and Mathematics. Registration records indicate course enrolment as follows: Chemistry (329). Physics (186).Mathematics (295). Chemistry and Physics (83), Chemistry and Mathematics (217), and Physics and Mathematics (63). How many students are taking all 3 subjects?
A contour line joins locations having the same height above the mean sea level. The following is a contour plot of a geographical region. Contour lines are shown at 25m intervals in this plot.
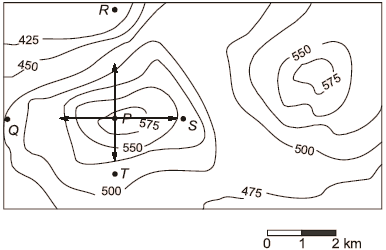
Q. Which of the following is the steepest path leaving from P?
Given (9 inches)1/2 = (0.25 yards) 1/2, which one of the following statements is TRUE?
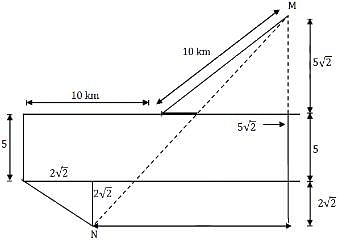
M and N start from the same location. M travels 10 km East and then 10 km North-East. N travels 5 km South and then 4 km South-East. What is the shortest distance (in km) between M and N at the end of their travel?
The number that least fits this set: (324, 441, 97 and 64) is _____.
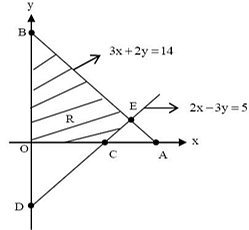
Find the area bounded by the lines 3x + 2y = 14, 2x - 3y = 5 in the first quadrant.
A straight line is fit to a data set (ln x, y). This line intercepts the abscissa at ln x = 0.1 and has a slope of −0.02. What is the value of y at x = 5 from the fit?
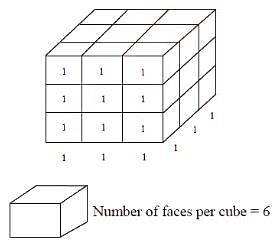
A cube of side 3 units is formed using a set of smaller cubes of side 1 unit. Find the proportion of the number of faces of the smaller cubes visible to those which are NOT visible.
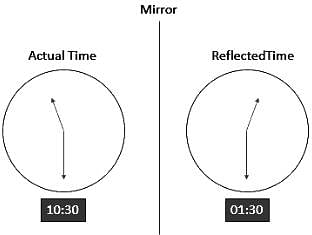
Two and a quarter hours back, when seen in a mirror, the reflection of a wall clock without number markings seemed to show 1:30. What is the actual current time shown by the clock?
A wire of length 340 mm is to be cut into two parts. One of the parts is to be made into a square and the other into a rectangle where sides are in the ratio of 1:2. What is the length of the side of the square (in mm) such that the combined area of the square and the rectangle is a MINIMUM?
It takes 10s and 15s, respectively, for two trains travelling at different constant speeds to completely pass a telegraph post. The length of the first train is 120 m and that of the second train is 150 m. The magnitude of the difference in the speeds of the two trains (in m/s) is _____.
|
18 docs|37 tests
|
|
18 docs|37 tests
|


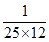
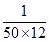
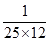
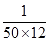
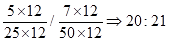
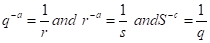 , the value of abc is _____
, the value of abc is _____