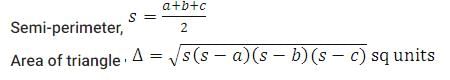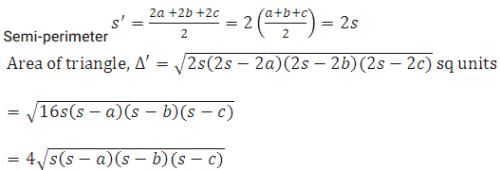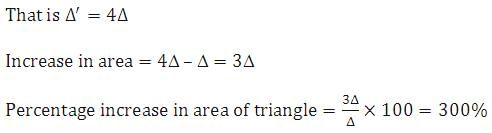Heron's Formula - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ

The length of each side of an equilateral triangle having an area of 4 √3 cm², is :

The area of a triangle is 150 cm² and its sides are in the ratio 3 : 4 : 5. What is its perimeter?

The altitude of an equilateral triangle of side 2 √3 cm is :

In a triangle ABC, BC = 5 cm, AC = 12 cm and AB = 13 cm. The length of the altitude drawn from B on AC is :

A triangle of area 9 × y cm² has been drawn such that its area is equal to the area of an equilateral triangle of side 6 cm. Then, the value of y is

In Δ PQR, side QR = 10 cm and height PM = 4.4 cm. If PR = 11 cm, then altitude QN equals :

The area of a right angled triangle is 30 cm² and the length of its hypotenuse is 13 cm. The length of the shorter leg is:

Area of a square with side x is equal to the area of a triangle with base x. The altitude of the triangle is :

A plot of land is in the shape of a right angled isosceles triangle. The length of the hypotenuse is 50 √2 m.The cost of fencing it at Rs. 3 per metre will be :

The perimeter of an isosceles triangle is equal to 14 cm, the lateral side is to the base in the ratio 5 : 4. The area of the triangle is

If the area of an equilateral triangle is 24√3 sq. m, then its perimeter is :

The ratio of the area of a square of side a and equilateral triangle of side a, is :

If every side of a trianlge is doubled, then increase in the area of the triangle is :

If the altitude of an equilateral triangle is √6 , then its area is :

The sides of a triangle are in the ratio of 3 : 4 : 5. If its perimeter is 36 cm, then what is its area?

If an equilateral triangle of area X and a square of area Y have the same perimeter, then :

A square and an equilateral triangle have equal perimeters. If the diagonal of the square is 12√2  cm, then the area of the triangle is :