IIT JAM Mathematics Mock Test- 3 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Mock Test- 3
Let V be the vector space of real polynomials of degree atmost 2. which defines a linear operator 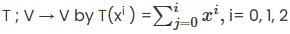 then the matrix of T–1 with respect to the basis (1, x, x2 ) is
then the matrix of T–1 with respect to the basis (1, x, x2 ) is
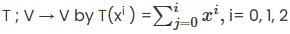 then the matrix of T–1 with respect to the basis (1, x, x2 ) is
then the matrix of T–1 with respect to the basis (1, x, x2 ) isLet p(x) be a non-zero polynomial of degree N the radius of convergence of the power series 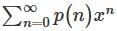
Consider the differential equation 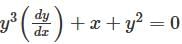 which of the following statements is true ?
which of the following statements is true ?
The solutions sin x and cos x of the differential equation 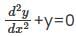 are
are
Let T: R2→ R3 be the Linear transformation whose matrix with respect to standard basis of R3 and R2 is  The T
The T
Consider the differential equation 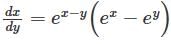 and y = 0 and
and y = 0 and 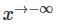 then y (loge 2) is;
then y (loge 2) is;
Let S be a closed surface and let denote the position vector of any point (x,y,z) measured from an origin O. then 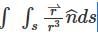 is equal to (if O lies inside S).
is equal to (if O lies inside S).
Let T: R3 → R3 be the Linear transformation whose matrix with respect to the standard basis 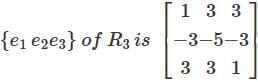 Then T
Then T
Consider the system of linear equations
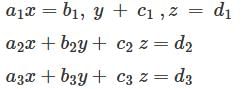
where ai bi ci di are real numbers for 1≤ i ≤3 if 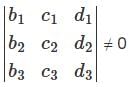 then the above system has
then the above system has
The mass of a solid right circular cylinder of height h and radius of base b, if density (mass per unit volume) is numerically equal to the square of the distance from the axis of the cylinder.is ;
Using the method of Lagrange multipliers the greatest and smallest value that the function f (x,y) = xy takes on the ellipse 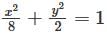 is
is
Let T : R3 → R3 be the linear transformation such that Y(1, 0, 1) = (0, 1 , –1) and T(2, 1, 1)= (3, 2, 1) Then T(–1, –2, 1)
Let V be the vector space of function 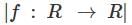 if W be its subsets then which of the following W is subspace of v
if W be its subsets then which of the following W is subspace of v
The function f : ℝ ℝ → satisfied  for all x, y ∈ and some constant c ∈ Then,
for all x, y ∈ and some constant c ∈ Then,
Let A be an n-by-n matrix with coefficients in F, having rows{a1, ..., an). Then which one of the statement is true for the matrix A?
Let y1(x) = 1 + x and y2(x) = ex be two solutions of y”(x) + p(x)y’(x) + Q(x)y(x) = 0 then the set of initial conditions for which the above differential equation has No solution is .
If f and g be continuous real valued functions on the metric space M. Let A be the set of all x ∈ M s.t. f(x) < g(x)
Value of the 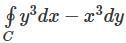 (where C are the two circles of radius 2 and 1 centered at the origin with positive orientation.)
(where C are the two circles of radius 2 and 1 centered at the origin with positive orientation.)
Which of the following transformations reduce the differential equation 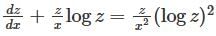 into the form
into the form 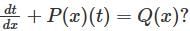


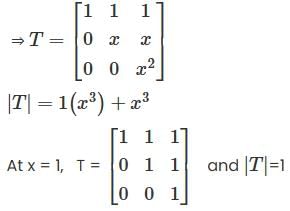
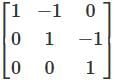

 and if
and if 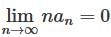 then
then 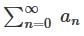 is
is 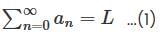
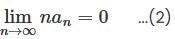
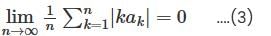
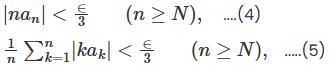
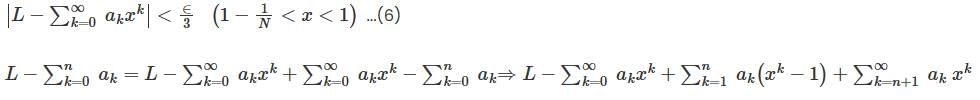
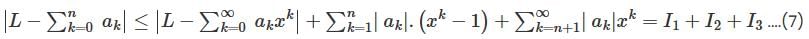
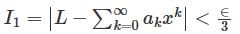
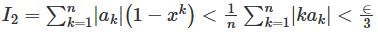
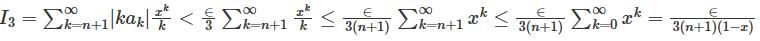
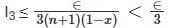
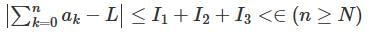
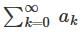 converges to L.
converges to L.
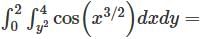
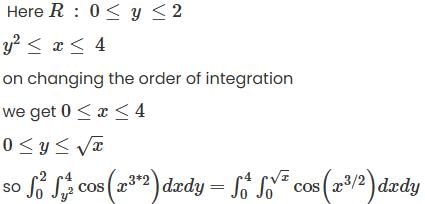
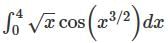
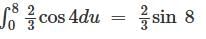
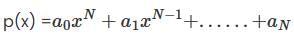
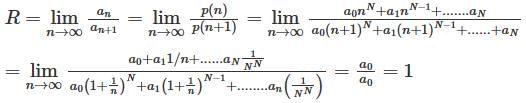
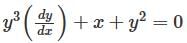
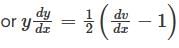
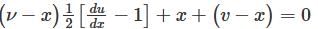
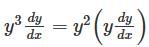
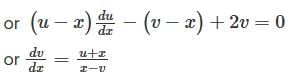
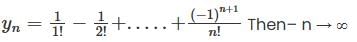
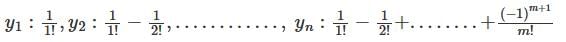
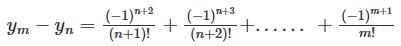
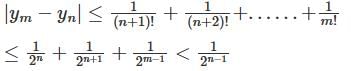
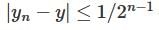
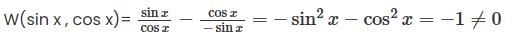
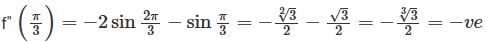

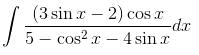
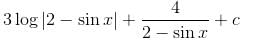
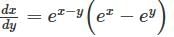
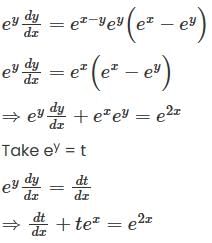

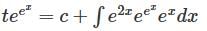
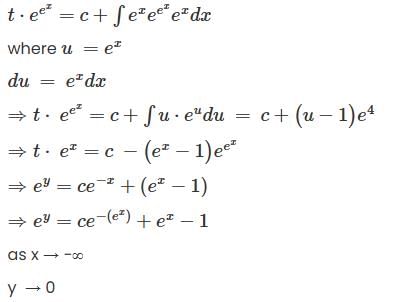
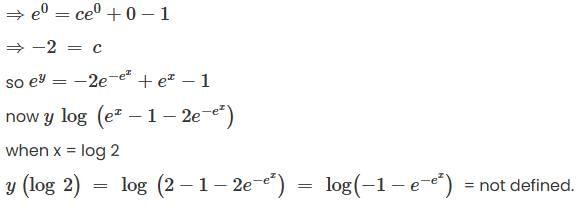
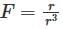 has a point to discontinuity at the origin. To remove this difficulty, let us enclose the origin by a small sphare Σ of radius ε.
has a point to discontinuity at the origin. To remove this difficulty, let us enclose the origin by a small sphare Σ of radius ε. 
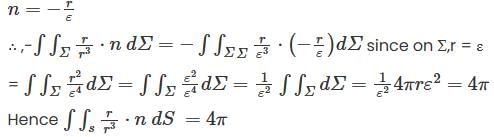
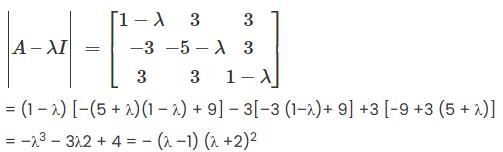
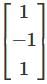
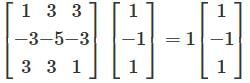
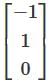
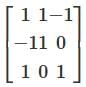

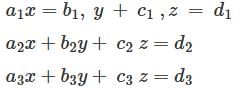
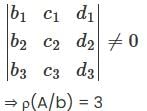
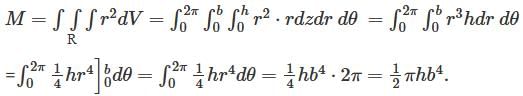
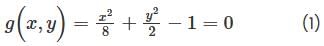
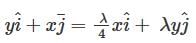
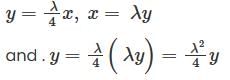

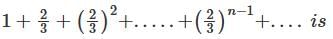
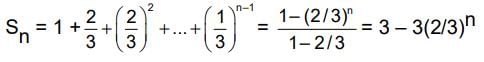
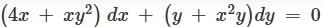 is
is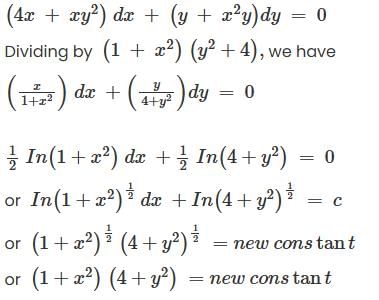
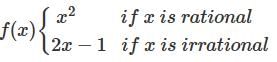 then,
then,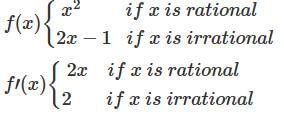
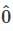 denote the zero polynomial, so
denote the zero polynomial, so 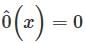 for every value of x.
for every value of x. 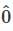 ∈ W, since
∈ W, since 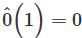 Suppose f. g ∈ W. Then f(1) = 0 and g(1) = 0. Also, for scalars a and b, we have
Suppose f. g ∈ W. Then f(1) = 0 and g(1) = 0. Also, for scalars a and b, we have 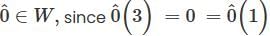 . Suppose f, g ∈ W. Them f(3) = f(1) and g(3) g(1). Thus, for any scalars a and b, we have
. Suppose f, g ∈ W. Them f(3) = f(1) and g(3) g(1). Thus, for any scalars a and b, we have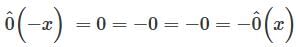 . Suppose f . g ∈ W. Then f(–x) = –f(x) and g(–x) = –g(x).
. Suppose f . g ∈ W. Then f(–x) = –f(x) and g(–x) = –g(x). 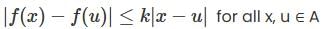

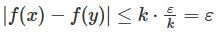
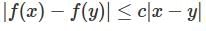
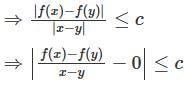

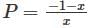

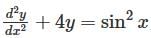 is given by ,
is given by , 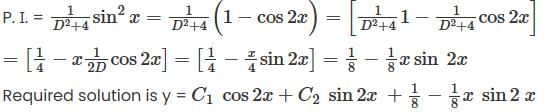
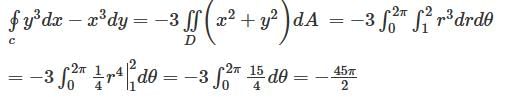

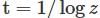 reduces the given differential equation into the form
reduces the given differential equation into the form  .
.















