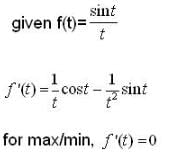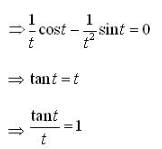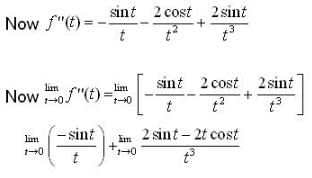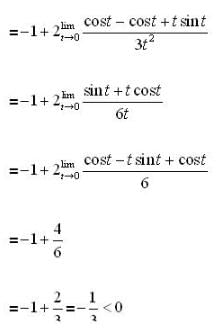IIT JAM Mathematics Practice Test- 13 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 13
What is the order of the differential equation given by dy / dx + 4y = sinx?
If y = x is a solution of x2y" + x y' - y = 0,then the second linearly independent solution of the above equation is.
Consider the differential equation y” + 9y = 0 with the boundary conditions, y(0) = 0, y(2π) = 1, then the differential equation has
The integrating factor of the differential equation,
(xy2 sin xy + y cosxy )dx + (x2y sin x y - x cos xy )dy - 0 is
The difference between the greatest and the least values of the function,
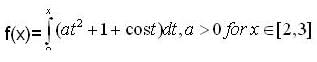
Let 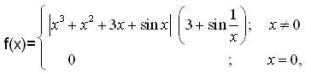
then number of points (where f(x) attains its minimum value )is ,
In [0,1] .Lagrange’s mean value theorem is NOT .applicable to
The orthogonal trajectories for the family of circles touching the y-axis at the origin is ,
The global maxima of f(x) = [2{-x2 + x + 1}] is , where {x} denotes fractional part of x and [-] denotes greatest integer function
Consider the differential equation 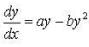 where a,b > 0 and y(0)=y0 when x → ∞ then solution y(x) tends to
where a,b > 0 and y(0)=y0 when x → ∞ then solution y(x) tends to
A function f is such that 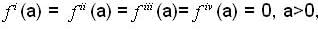 and f has local maximum of -20 at x = a , then f(x) may be ,
and f has local maximum of -20 at x = a , then f(x) may be ,
Consider the differential equation 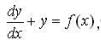 where
where
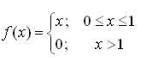 and y(0) = 0, if y(x) be the continuous solution on [ 0, ∞) then
and y(0) = 0, if y(x) be the continuous solution on [ 0, ∞) then
The initial value problem 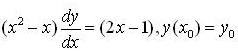 has a unique solution if ( x0,y0 ) equals,
has a unique solution if ( x0,y0 ) equals,
The polynomial function f(x) of degree 6 ,which satisfies,
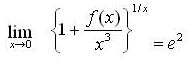
and has local maxima at x =1 and local minimum at x = 0 and x =2, is
The set of all the values of K for which the point of minimum of the function f(x) = 1 + K2x - x3, satisfy the inequality
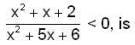
If 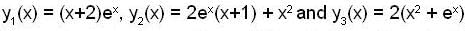 are three solutions of a non - homogeneous linear differential equation
are three solutions of a non - homogeneous linear differential equation 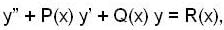 where P(x), Q(x) and R(x) are continuous function on [a, b] with a > 0, then its particular solution w.r. to the conditions y(0) = 0 y.O) = 1
where P(x), Q(x) and R(x) are continuous function on [a, b] with a > 0, then its particular solution w.r. to the conditions y(0) = 0 y.O) = 1
Let y(x) be the solution of the different equation 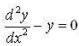 such that y(0) = 2 and y'(0) = 2α. Then the values of
such that y(0) = 2 and y'(0) = 2α. Then the values of  such that the in infimum of the set
such that the in infimum of the set 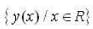 is greater than or equal to1 , are
is greater than or equal to1 , are
The differential equation satisfied by the system of parabolas y2 = 4a(x+ a) is
if 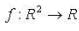 is defined by
is defined by
Consider the differential equation 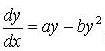 , where a,b > 0 and y(0) = y0 when
, where a,b > 0 and y(0) = y0 when
 , then solution y(x) tends to
, then solution y(x) tends to
Let y(x) be the solution of the differential equation,
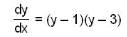
satisfying the condition y(0) = 2. then which of the following is not true ?
consider the following's two inqualities as:
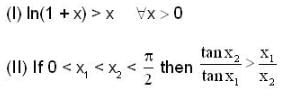
then which one is true?
Consider the follwing two statements
(I) for all x in [0,1] , let the second derivative f"(x) of a function f(x) exist and satisfy 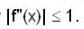 if f(0) = f(1) then
if f(0) = f(1) then 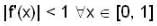

then which one is true?
Let y(x) be a continous solution of the intial value problem
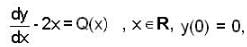
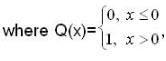
then which of the follwoing is true ?
A differentiable function f(x) has relative minimum at x = 0, then the function y = f(x) +ax+ b, has a relative minimum at x = 0 for


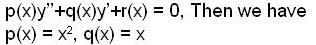 and given y = x is a solution of (1)
and given y = x is a solution of (1)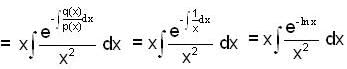
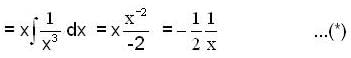 2nd L.l. solution = 1/x
2nd L.l. solution = 1/x
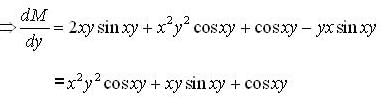
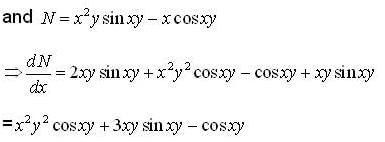
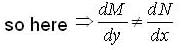
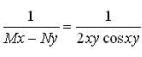
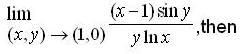
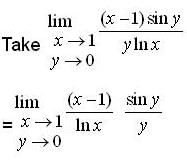
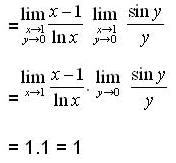
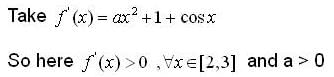
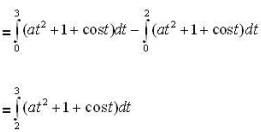
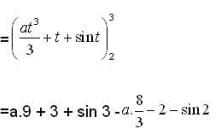
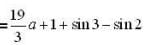
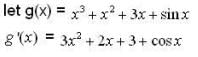
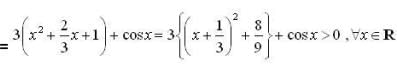
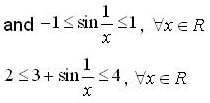
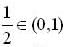 but in other part critical point
but in other part critical point 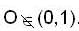 . then we can say that function in option (B),(C) and (D) are continuous on [0,1] and differentiable in (0,1).
. then we can say that function in option (B),(C) and (D) are continuous on [0,1] and differentiable in (0,1).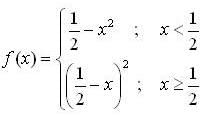
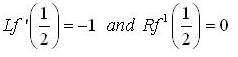
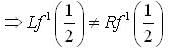
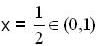
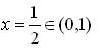
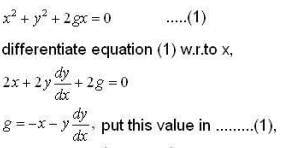
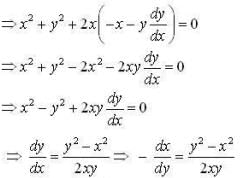
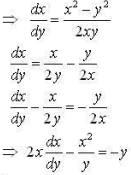
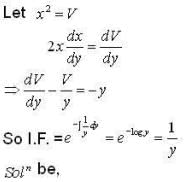
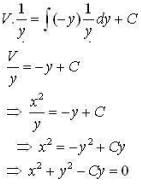
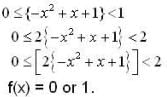
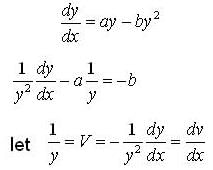
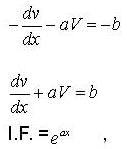
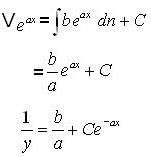
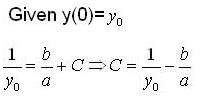
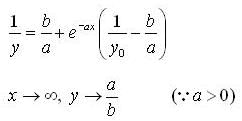



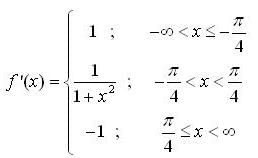
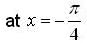 the sign of f has no changes
the sign of f has no changes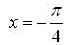 be a point of infection.
be a point of infection.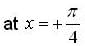 the sign of f has changes from +ve to -ve
the sign of f has changes from +ve to -ve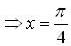 be the point of local maxima and clearly it be the only point at which f has local maximum value.
be the point of local maxima and clearly it be the only point at which f has local maximum value.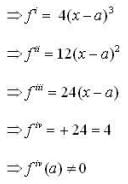
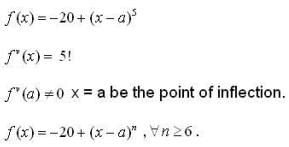
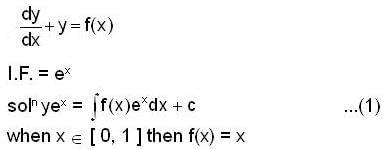
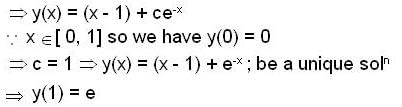
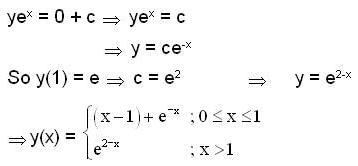
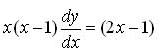
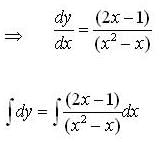
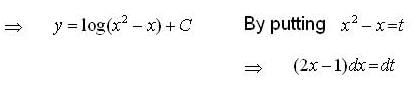
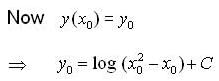
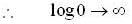
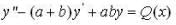 is
is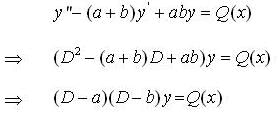
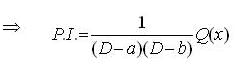
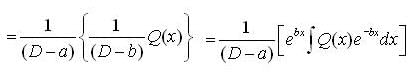
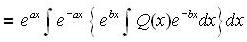
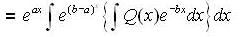
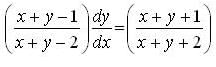 given that y =1 when x =1 is
given that y =1 when x =1 is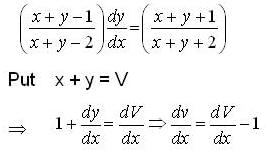
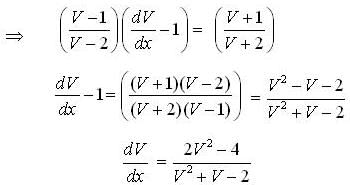
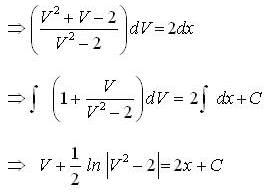
 Given y (1) = 1
Given y (1) = 1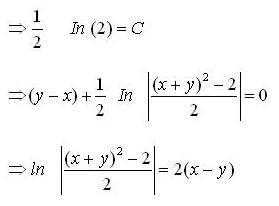

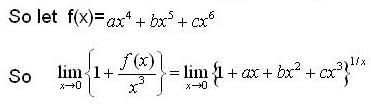
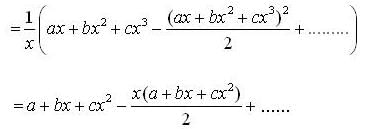
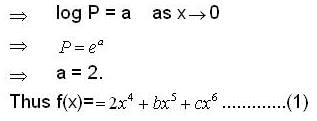
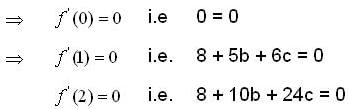
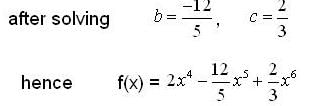
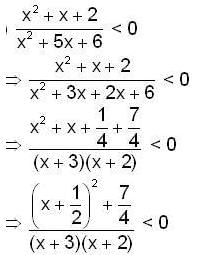
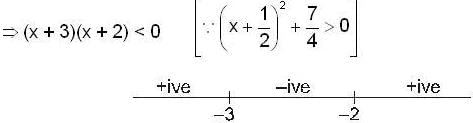
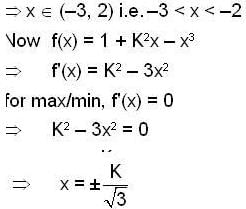
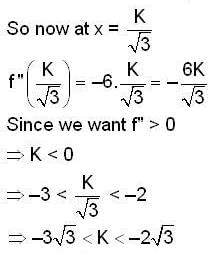
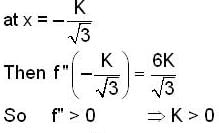
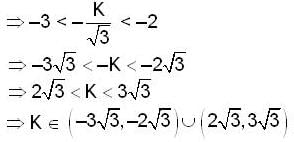
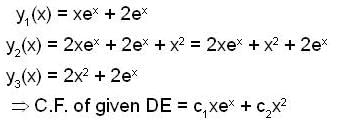
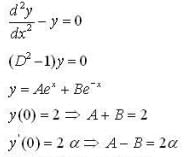
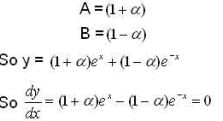
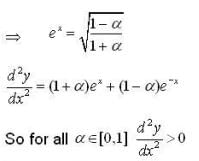

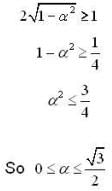
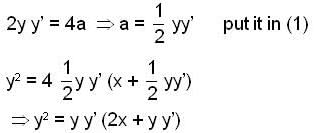
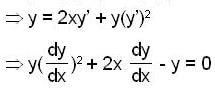
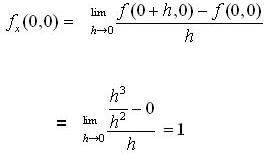
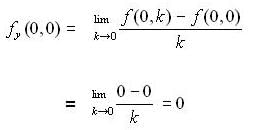

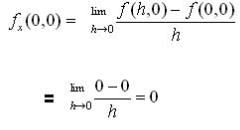


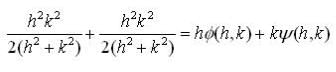
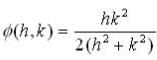 and
and 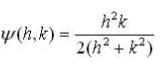

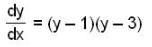
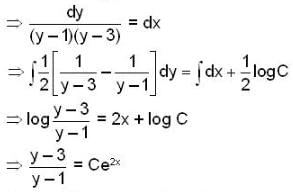
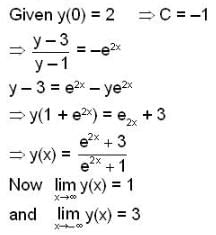
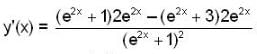
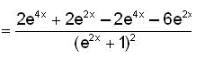
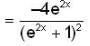

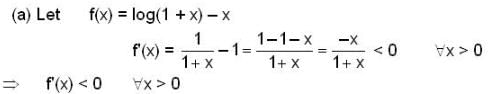
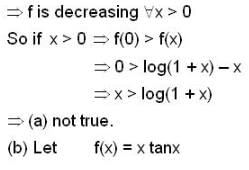
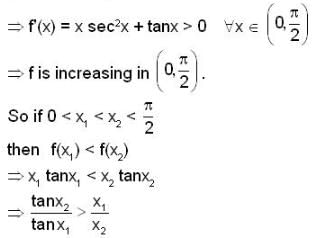
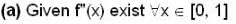
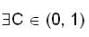
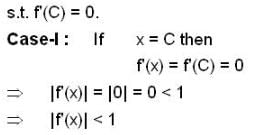
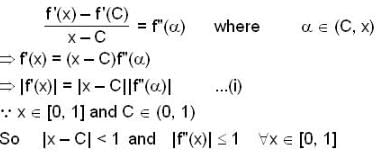
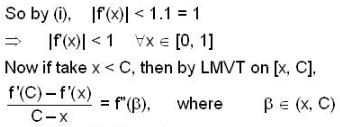
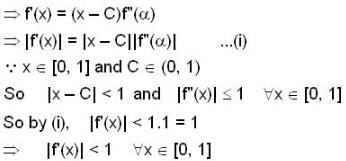
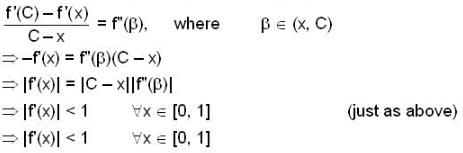
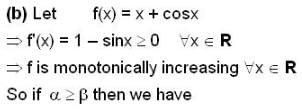
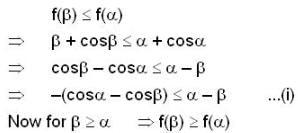
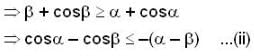
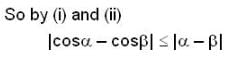
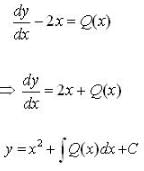
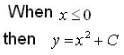
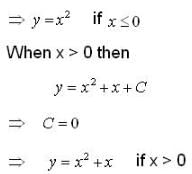
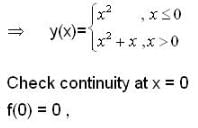

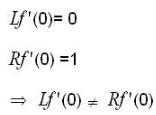
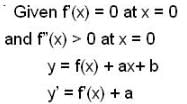
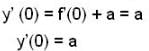
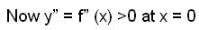
 has
has