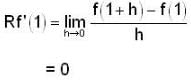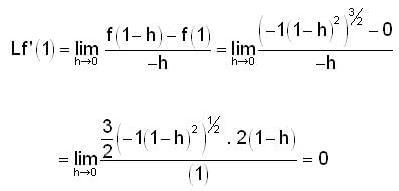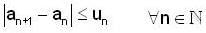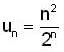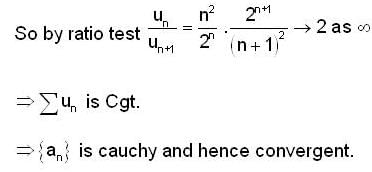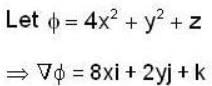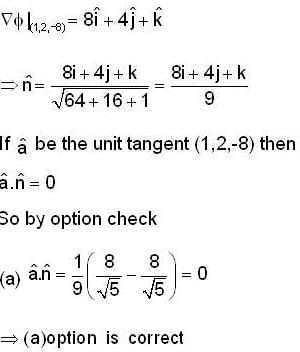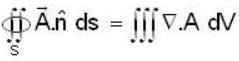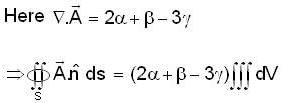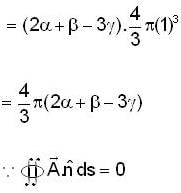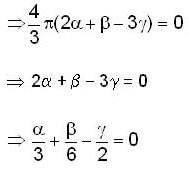IIT JAM Mathematics Practice Test- 19 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 19
For what value of n, double integral 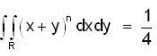 where region R is bounded by x + y = 1 in the first quadrant?
where region R is bounded by x + y = 1 in the first quadrant?
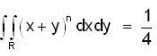 where region R is bounded by x + y = 1 in the first quadrant?
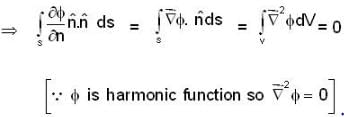
where region R is bounded by x + y = 1 in the first quadrant?If 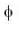 is harmonic in V then for any closed surface S consisting the volume V, the integral
is harmonic in V then for any closed surface S consisting the volume V, the integral 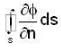 is equal to
is equal to
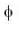 is harmonic in V then for any closed surface S consisting the volume V, the integral
is harmonic in V then for any closed surface S consisting the volume V, the integral 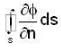 is equal to
is equal to The transformation T : R3 → R2 defined by,
T(x,y,z) = (x +y, y+z) is,
The radius of convergence of power series 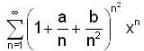 is,
is,
A cauchy sequence in Q which does not have a limit in Q is
Suppose the matrix  has a certain complex no. λ ≠ 0 as an eigenvalue. Which of the following no. must also be an eigenvalue of A?
has a certain complex no. λ ≠ 0 as an eigenvalue. Which of the following no. must also be an eigenvalue of A?
If A and B are unbounded subsets of R, which of the following is necessarily unbounded?
Let f: R3 → R3 be the matrix transformation defined by
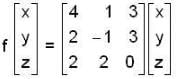 if we have,
if we have,
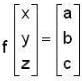 then for the solution, i.e. for the existence of values of x,y and z.
then for the solution, i.e. for the existence of values of x,y and z.
Find the total no. of elements of order 12 in a cyclic group of order 60.
Which of the following pair of groups is isomorphic to each other?
If G is a group, then for every a ∈ G, what is (a−1)−1?
Let f' (sin x) < 0 and f' (cos x) > 0. 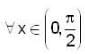 and g (x) = f (sin x) + f (cos x) then which of the following is true?
and g (x) = f (sin x) + f (cos x) then which of the following is true?
Let 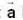 be a constant vector and V is the volume enclosed by the closed surface S. The integral
be a constant vector and V is the volume enclosed by the closed surface S. The integral 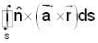 is equal to (where ñ is the outward going unit normal to the surface S)
is equal to (where ñ is the outward going unit normal to the surface S)
If 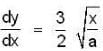 then find the length of the curve y = f(x) from the vertex (0, 0) to the point (a, a).
then find the length of the curve y = f(x) from the vertex (0, 0) to the point (a, a).
Given 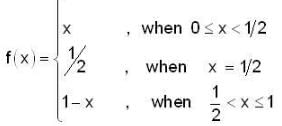
and G(x) = (x - 1/2)2, x ∈ R
what is the area of the portion bounded between G(x) and f(x) inn the interval 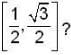
 are three vectors with magnitude |a| = 4, |b| = 4, |c| = 2 and such that
are three vectors with magnitude |a| = 4, |b| = 4, |c| = 2 and such that  is perpendicular to
is perpendicular to 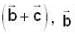 is perpendicular to
is perpendicular to  is perpendicular to
is perpendicular to 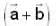 , then
, then 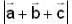 is equal to
is equal to
If 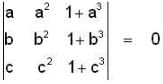 and
and 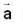 = (1, a, a2)
= (1, a, a2)
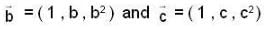 are non-coplanar vectors, then abc is equal to
are non-coplanar vectors, then abc is equal to
The differential equation 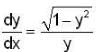 determines a family of circles with,
determines a family of circles with,
The orthogonal trajectories of the hyperbolas xy = c is
Let P : R → R be a polynomial of the form P(x) 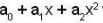 with
with 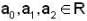 and
and 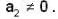
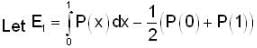
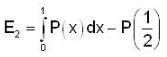
If |x| is the absolute value of x ∈ R, then
A: R6 → R6 be a linear transformation such that A2 = 0, then the rank of A is
Let V be the space of twice differentiable functions on R satisfying f'' - 2f' + f = 0. Define T : V → R2 by T(f) = (f'(0), f(0)), Then T is
Let f : 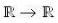 denote the function defined by f(x) =
denote the function defined by f(x) = 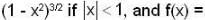
 Which of the following statement is correct?
Which of the following statement is correct?
Let {an} be a sequence of real no. such that 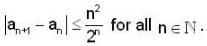 Then
Then
Consider the surface corresponding to the equation 4x2 + y2 + z = 0 A possible unit tangent to this surface at the point (1, 2, -8) is
If the surface integral of the field 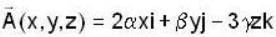 over the closed surface of an arbitrary unit sphere is to be zero, then the relationship between
over the closed surface of an arbitrary unit sphere is to be zero, then the relationship between 


 <3> in Z30
<3> in Z30  Z12 is
Z12 is <3> is a subgroup of order 24 in Z30
<3> is a subgroup of order 24 in Z30  Z12.
Z12.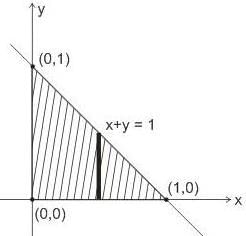
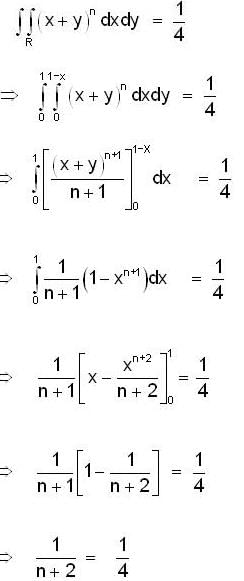

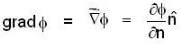
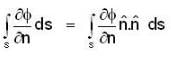

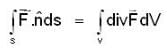
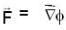
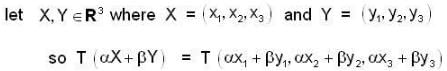
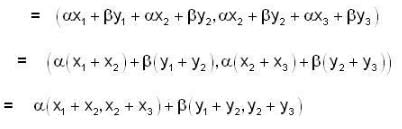
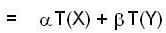
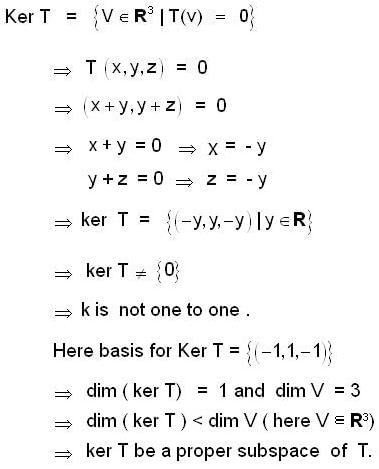
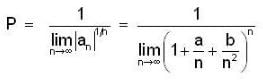
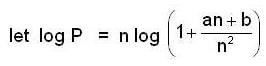
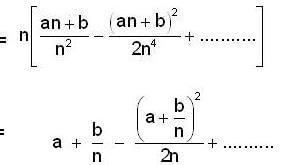
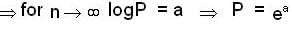
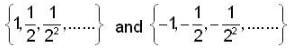 and both are converging to 0.
and both are converging to 0. 
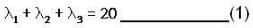
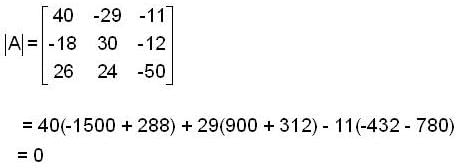
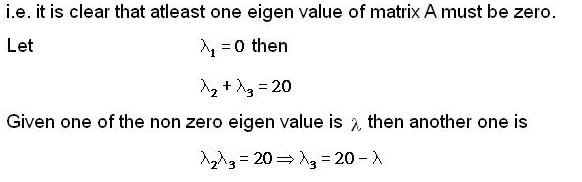
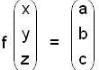

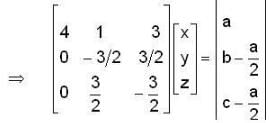
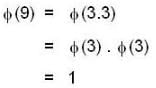
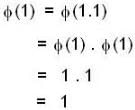


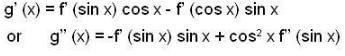
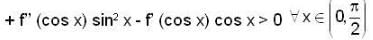
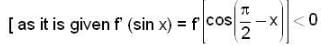
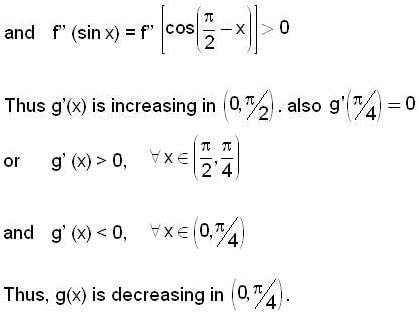
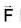 be any vector function then by the result we know that
be any vector function then by the result we know that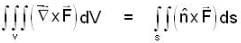

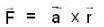
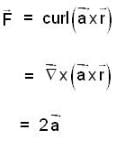
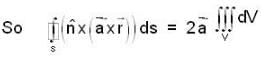
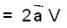
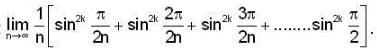
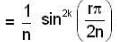 where r varies form 1 to n.
where r varies form 1 to n.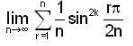
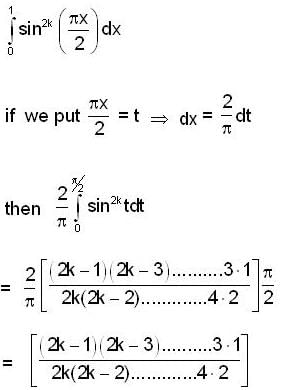
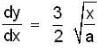
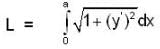
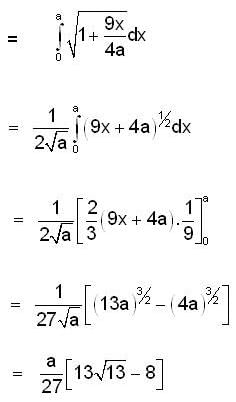
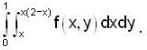
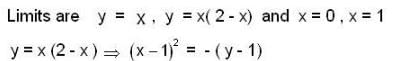
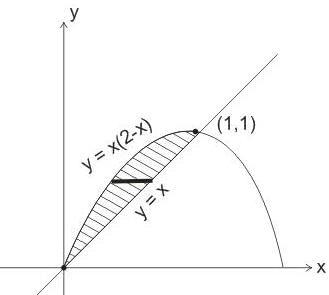
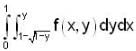
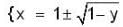 the bounded region takes values less than 1.}
the bounded region takes values less than 1.}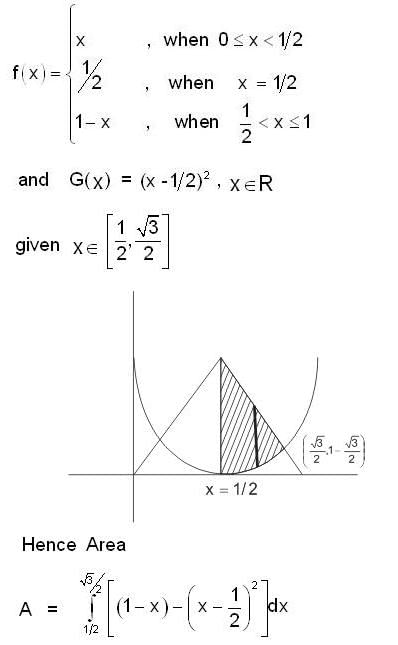
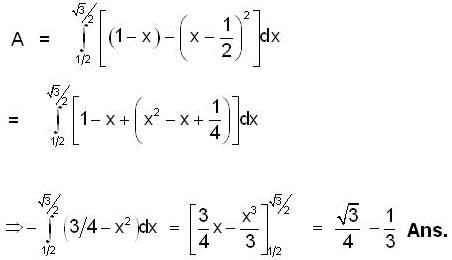
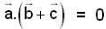
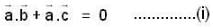
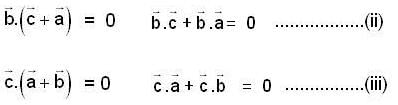
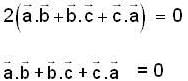
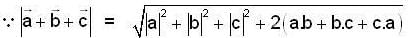
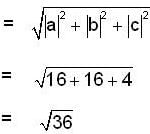

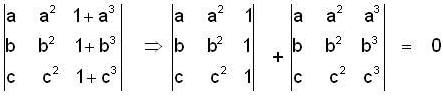
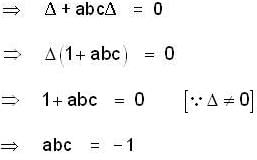
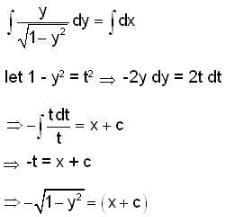
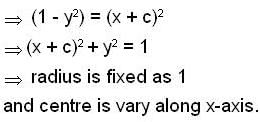
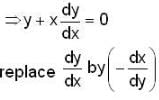
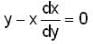 : DE of required O.T
: DE of required O.T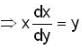
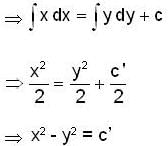
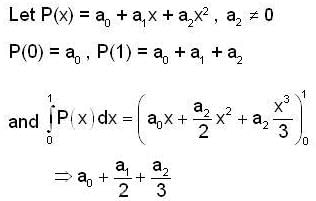
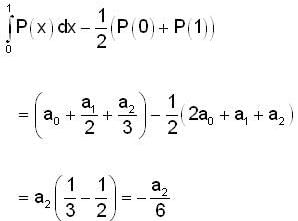
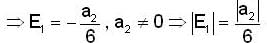
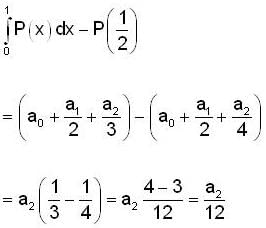
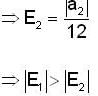





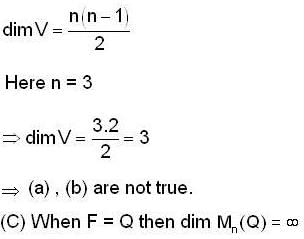
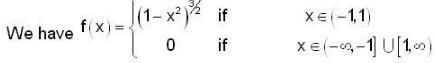
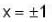 and hence on R
and hence on R