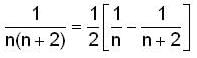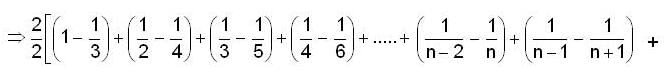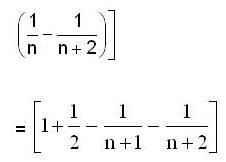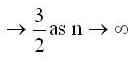IIT JAM Mathematics Practice Test- 6 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 6
The linear operation L(x) is defined by the cross product L(x) = bx, where b = [0, 1, 0] T and X = [x1 x2, x3]T are three dimensional vectors. The 3 x 3 matrix M o f the operation satisfies 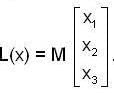 Then the eigen values of M are
Then the eigen values of M are
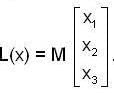 Then the eigen values of M are
Then the eigen values of M areFind the condition when the following system of linear equations have no solution.
x + 4z = 2
x + w = 0
x +y = 0
x + 2y + 3w + tz = s
The value of the determinant of nth order, being given by  is
is
 is
isThe system of linear equations
x + y + z = 2, 2x + y - z = 3, 3x + 2y + kz = 4 has a unique solution, if
For the matrix 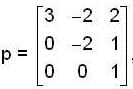 one of the eigen value is equal to -2. Which of the following is an eigen vector?
one of the eigen value is equal to -2. Which of the following is an eigen vector?
The linear system has
x1 + 2x2 - 3x4 + x5 = 2
x1 + 2x2 + x3 - 3x4 + 2x6 + x5 = 3
x1 + 2x2 - 3x4 + 2x5 + x6 = 4
3x1 + 6x2 + x3 - 9x4 + 4x5 + 2x6 = 9
The System of equations,
x + y + z = 8
x - y + 2z = 6
3x + 5y+ 7z= 14 has,
Suppose
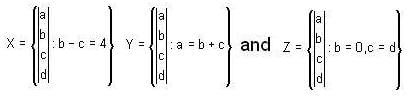
Which of these subsets of the vector space R4 is/are subspace (s) ?
Which of the following sets is not linearly independent?
if  is a basis of C3(C), then which of the following set is also a basis of C3(C) ?
is a basis of C3(C), then which of the following set is also a basis of C3(C) ?
Let y(x) be the solution of differential equation,
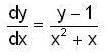
which satisfy the condition y(1) = 0. Then which of the following’s is true ?
For what value of k , the function 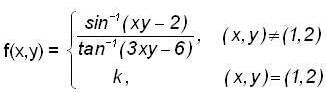 is continuous ?
is continuous ?
If 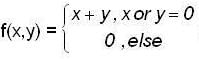 Then, the directional derivative at c = (0,0) along the direction u (a,b),a ≠ 0 ≠ b is
Then, the directional derivative at c = (0,0) along the direction u (a,b),a ≠ 0 ≠ b is
Let T be linear operator on R3- the matrix of which in the standard ordered basis is 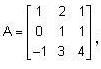 Then
Then
If the Linear Transformation is defined as 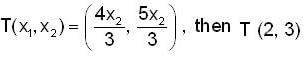 and T (1, 0) is equal to,
and T (1, 0) is equal to,
The "Cyclic" transformation T is defined by T(v1,v2,v3) = (v2,v3,v1), then T100 (v) is not equal to
Let L : P2 -> P2 be the linear transformation defined as, L (at2 + bt + c) = (a+ 2b)t+(b+ c), then,
(I) - 4t2 + 2t - 2 is in th e ker (L)
(II) Basis for ker (L) is 2t2 - 1+ 1
which of the following options is / are not true.
Let V be the vector space of all polynomial functions of degree ≤ 2 from the field of real numbers R into itself. Let {f1, f2, f3} be an ordered basis of V(R), where f1(x) = 1, f2(x) = x + 1, f3(x) = (x + 1)2, then the co-ordinates of 1 + x + x2 in this basis is
If 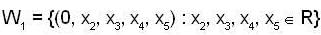 and
and 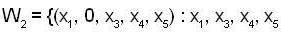
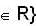
be subspaces of R5, then dim 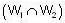 is equal to _______.
is equal to _______.
Let M2x2 (R) be the vector space of all 2 * 2 matrices over R
Let
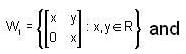
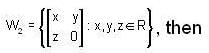
dim 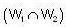 is equal to ________ .
is equal to ________ .
Find the dimension of the subspace 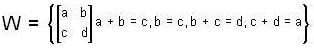 of M2x2 (R)
of M2x2 (R)
Given the linear transformation

Find rank of T.
If 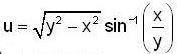 then the value of the expression
then the value of the expression 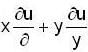 at the point ( 1 ,2 ) i s -----------
at the point ( 1 ,2 ) i s -----------
Find the value of the 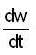 where w = xy + yz + zx, x = t2,y = tet z = te-t at t = 0
where w = xy + yz + zx, x = t2,y = tet z = te-t at t = 0


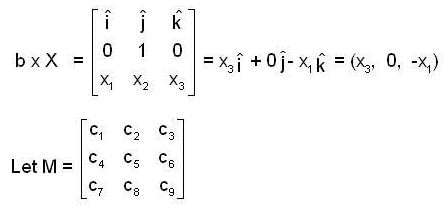
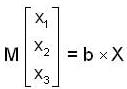

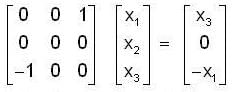
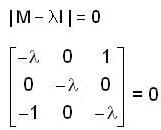
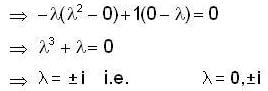
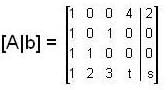


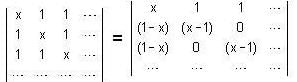
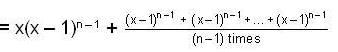
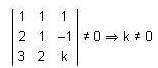
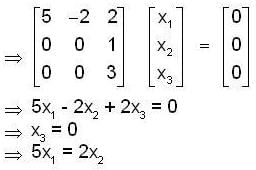
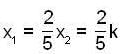
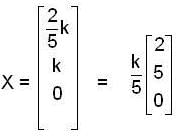


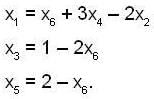
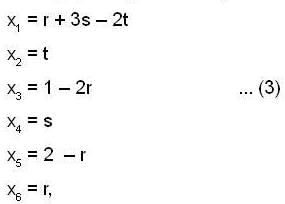

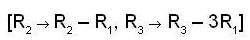
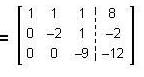
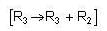
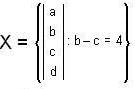
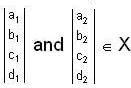 and α, β, ∈ F with b1 - c1 = 4 and b2 - c2 = 4
and α, β, ∈ F with b1 - c1 = 4 and b2 - c2 = 4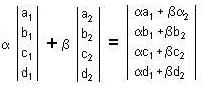
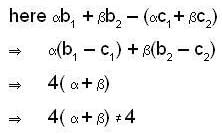
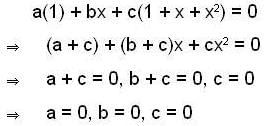
 be any finite subset of S having n vectors .
be any finite subset of S having n vectors .
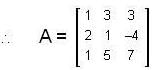
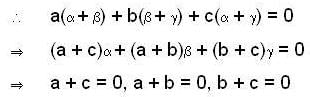 (Since, α, β, and γ are independent)
(Since, α, β, and γ are independent)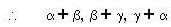 are linearly independent
are linearly independent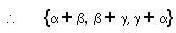 is the basis of C3
is the basis of C3

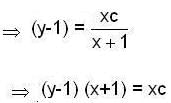
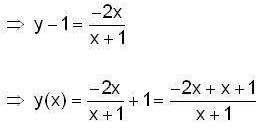
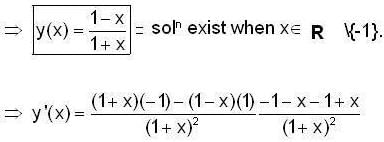
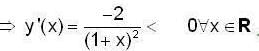
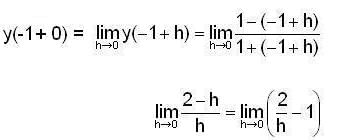
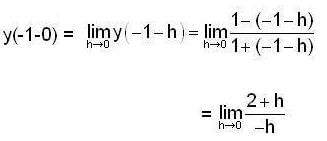
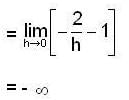
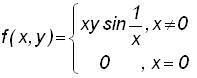 Then,
Then,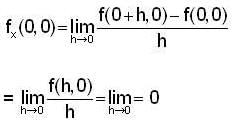
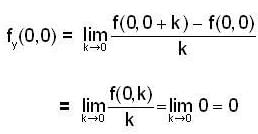
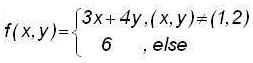 then
then 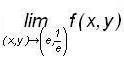 is
is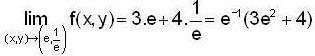

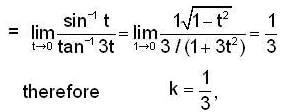
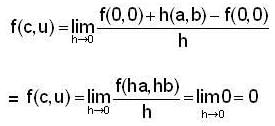
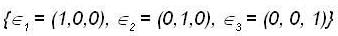
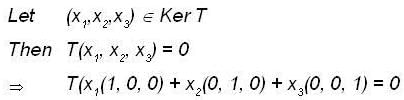
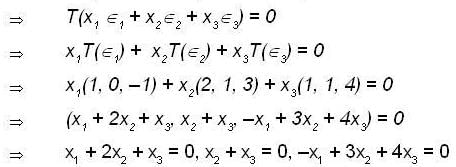
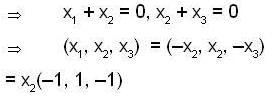
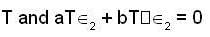
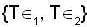 is a linearly in dependent set in Range T .As dim Range T = 2, {(1,0, -1), (2, 1, 3)} is basis of Range T.
is a linearly in dependent set in Range T .As dim Range T = 2, {(1,0, -1), (2, 1, 3)} is basis of Range T.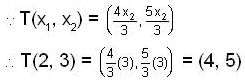
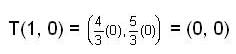
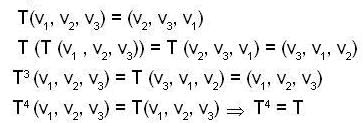
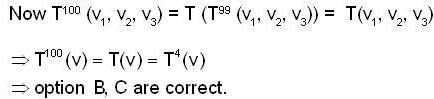

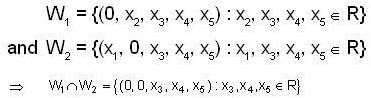 ∴ Which is subspace of R5 and clearly
∴ Which is subspace of R5 and clearly 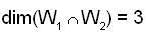
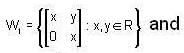
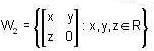
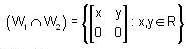
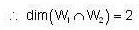

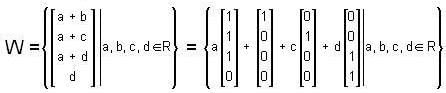
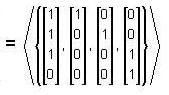
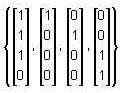 is a linearly independent set, thus it forms a basis of W. Thus, W is a subspace of C4 with dimension 4.
is a linearly independent set, thus it forms a basis of W. Thus, W is a subspace of C4 with dimension 4.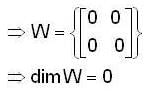

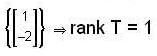
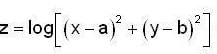 find
find 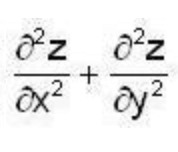
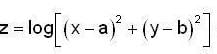 then
then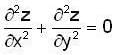 and
and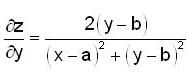
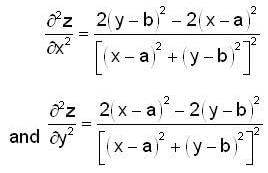
 except at (a,b)
except at (a,b) 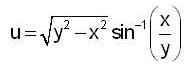
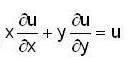
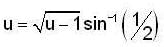
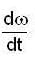 where ω = x2 + y2,
where ω = x2 + y2, 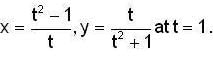
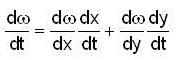
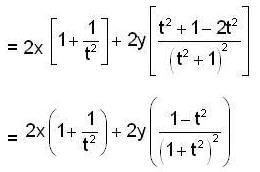
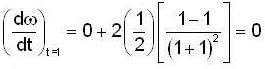
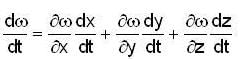
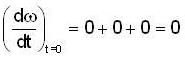
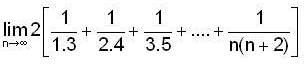 is equal to _______________
is equal to _______________