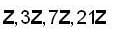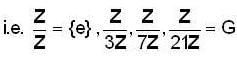IIT JAM Mathematics Practice Test- 7 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 7
If G be an one empty set
(1) a(bc) = (ab)c for all a, b, c ∈ G
(2) For any a, b ∈ G, the equations ax = b and ya = b have solutions in G.
then
then
If p is a prime number and G is non-abelian group of order p3, then the centre of G has
If each of the following statements is true, then P ⇒ ~q, q ⇒ r, ~r
Let Sn be the symmetry group of n letters and assume that it abelian. Then.
Let G be an infinite cyclic group and H is its subgroup. Which one of the following is correct ?
If H and K are finite subgroups of a group G then
If n is the order of element a of group G then am = e, an identity element iff -
A group (G, *) has 10 elements. The minimum number of elements of G, which are their own inverse is
(i) Every subgroup of a cyclic group is also cyclic.
(ii) Every proper subgroup of an infinite cyclic group is infinite.
(i) Every Quotient group of an abelian group is abelian
(ii) Every Quotient group of a cyclic group is not cyclic.
Let T = { z ∈ c : | z | = 1} then (T, x) is a group which o f the following are not subgroup of (T, x)
(1) Every group of prime order is not simple.
(2) A subgroup H of a group G is normal, iff
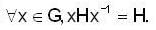
Let G be the group of non zero real numbers under multiplication
(1) {x ∈ G | x = 1 or x is irrational}
(2) {x ∈ G | x ≥ 1}
Which one of the following statements is true?
If H and K are subgroup of a group G, then which of the following is FALSE ?
Let G be the set of all 2 x 2 matrices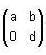 where ad ≠ 0 under matrix multiplication and
where ad ≠ 0 under matrix multiplication and 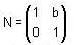 where a, b, c, d are real number, then which of the following statements is/are correct?
where a, b, c, d are real number, then which of the following statements is/are correct?
Let s = (1 3 5 7 11) (2 4 6) ∈ S11 then find the smallest positive integer n, such that sn = s37.
Let G be a group of 35 elements. Then the largest possible size of a subgroup of G other than G itself is ______.
Consider the system of equations x + y + z = 1, 2x + 3y + 2z = 1, 2x + 3y + (a2 - 1)z = a + 1 then
___________ is the order of {3} in the multiplicative group of integers modulo 5.
{0, 1, 2, 3, 4, 5} is a group under addition modulo 6, then the order of 1 is ___________.
The number of generators of a cyclic group of order 12 is ________.
The total number of proper subgroups of the group (Z, +) of integers ________.
Total number of non abelian groups of order 23 . 34. 5 is __________.


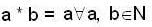
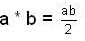 for all a, b ∈ Q. This is not a group since inverse of element 0 ∈ Q does not exist.
for all a, b ∈ Q. This is not a group since inverse of element 0 ∈ Q does not exist.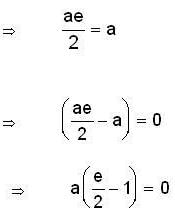
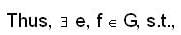
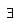 some x, y in G s.t.,
some x, y in G s.t.,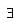 e ∈ G, s.t., ae = ea = a
e ∈ G, s.t., ae = ea = a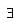 some a1 ∈ G satisfying the above relations ⇒ a has an inverse. Thus each element has inverse and, by definition, G forms a group.
some a1 ∈ G satisfying the above relations ⇒ a has an inverse. Thus each element has inverse and, by definition, G forms a group.
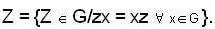
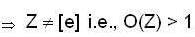
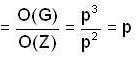
 a decomposition of K into disjoint right cosets of D in K and
a decomposition of K into disjoint right cosets of D in K and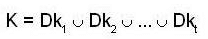

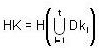 and since
and since 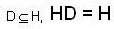
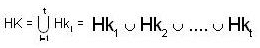
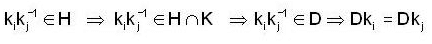
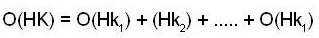
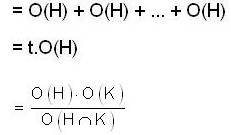
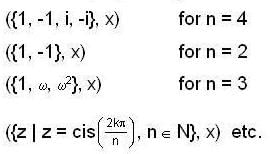
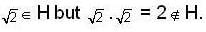

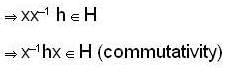
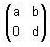
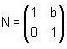 Where a, b, d are real numbers, the N will be a subgroup of G and according to the definition of normal subgroup. A subgroup H of a group G is said to be a normal subgroup of G if for every x ∈ G and for every h ∈ H, xHx-1 ∈ H, so here, N is a subgroup of G and N will be normal in G.
Where a, b, d are real numbers, the N will be a subgroup of G and according to the definition of normal subgroup. A subgroup H of a group G is said to be a normal subgroup of G if for every x ∈ G and for every h ∈ H, xHx-1 ∈ H, so here, N is a subgroup of G and N will be normal in G.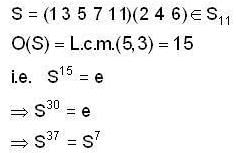
 .
.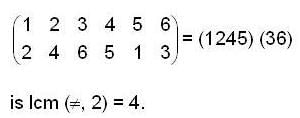 Because 0(1245) = 4 and o(36) = 2
Because 0(1245) = 4 and o(36) = 2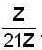
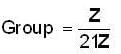
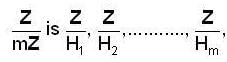
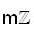
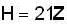 ’ then its subgroups are
’ then its subgroups are