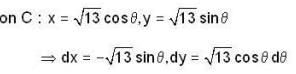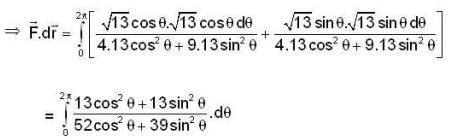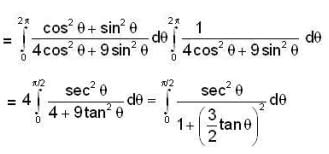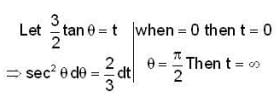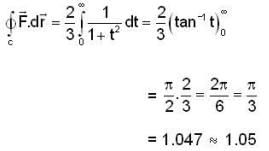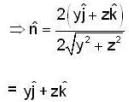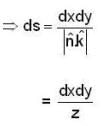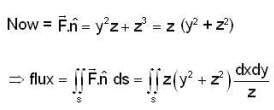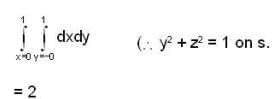IIT JAM Mathematics Practice Test- 8 - Mathematics MCQ
30 Questions MCQ Test - IIT JAM Mathematics Practice Test- 8
Let G be a group. Suppose a, b ∈ G such that,
(i) ab = ba
(ii) (0(a), 0(b)) = 1.
If Ha ≠ Hb ⇒ aH ≠ bH then a sub group H of G is
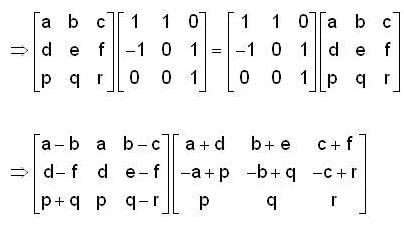
A subgroup H of a group G is normal subgroup if:
Let H and N be subgroup and normal subgroup of a group G respectively then
Let N1 and N2 be two normal subgroup of a group G then 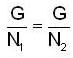 if
if
The number of 2 x 2 matrices over Z3 (The field with three elements) with determinant 1 is ________
If G is a group, Z its center and if G/Z is cyclic then G
Let G be a non abelian group then the m apping f : G→ G given by 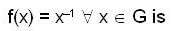
If the subgroup H of G contain the derived subgroup G' of G then H is normal in G and G/H is abelian then
If  Then, which one of the follow ing is correct ?
Then, which one of the follow ing is correct ?
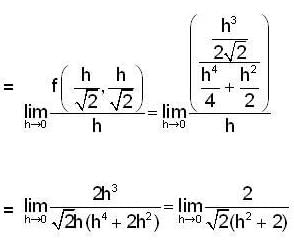
Let f : R2 -> R be defined by
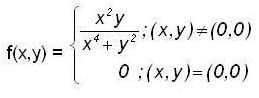
then ,the directional derivative of f at (0,0) in the direction of the vector 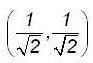 is
is
Each of the six players participating in a chess competition will play one match with each other player. Tell us how many matches will be played in the entire competition-
Which of the following statements is/are true ?
Find the number of element of order 10 in Z30‘
Let U(n) be the set of all positive integers less than n and relatively prime to n. Then, U(n)isagroup under multiplication modulo n. For n = 248, find the number of elements in U(n).
Let G be a finite group of order 200. Then find total number of subgroup of G of order 25.
In a non-abelian group, the element a has order 108. Then find order of a42.
Find the order of Aut (G), where G is a group with 65 elements.
 is equal to ... (correct upto two decimal places).
is equal to ... (correct upto two decimal places).
Let P3(x) be a vector space of all real polynomals with degree at most 3. consider the subspaces as,
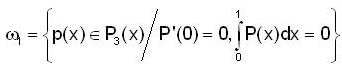 and
and 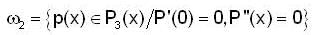 then the dim of
then the dim of 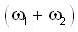 is ___________.
is ___________.
Let M3 R be the vector space of 3x3 real matrices . Let V be a subspace of M3 R defined by
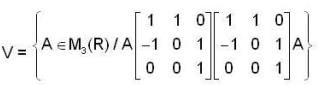
Then the dimension of V is ____________
Let 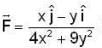 be a planar vector field. Let
be a planar vector field. Let 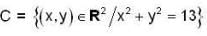 be the circle oritented anti- clockwise. Then
be the circle oritented anti- clockwise. Then 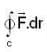 is equal t o ______________ (Correct upto two decimal places).
is equal t o ______________ (Correct upto two decimal places).
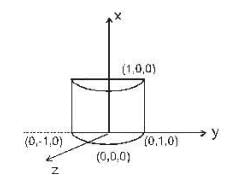
The flux of vector field 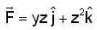 outward through the surface S cut from the cylinder
outward through the surface S cut from the cylinder  by the planes x = 0 and x = 1 is ___________ .
by the planes x = 0 and x = 1 is ___________ .


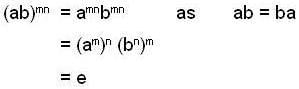
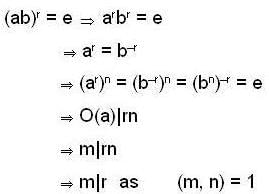
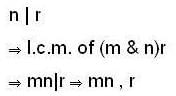
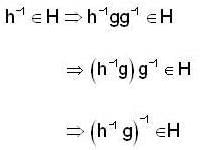

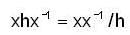
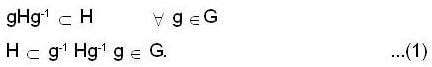
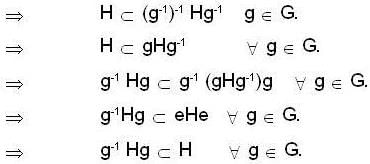
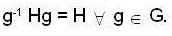

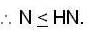
 ..(1)
..(1)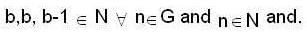
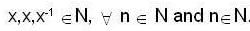
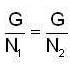 then we are to prove that N1 = N2 we have
then we are to prove that N1 = N2 we have 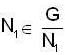 but
but 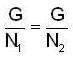 therefore
therefore 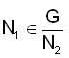 that is N1 is equal to some coset of N2 in G. But two cosets of N2 in G are either disjoint or identical since e ∈ N1 and e ∈ N2 th e re fo re N1 and N2 are not disjoint so we must have N1 = N2.
that is N1 is equal to some coset of N2 in G. But two cosets of N2 in G are either disjoint or identical since e ∈ N1 and e ∈ N2 th e re fo re N1 and N2 are not disjoint so we must have N1 = N2.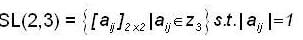
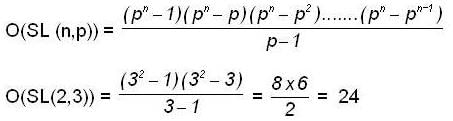
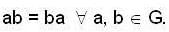
 z1 ∈ Z such that a ∈ z1 gm
z1 ∈ Z such that a ∈ z1 gm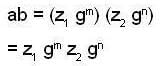
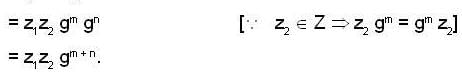 Again
Again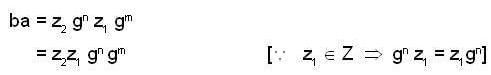
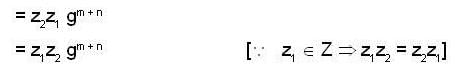
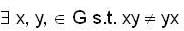
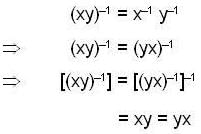
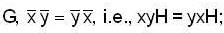 his is the same as to say that fo r all x, y in
his is the same as to say that fo r all x, y in  i.e., that H contains every commutator [x, y], (x, y ∈ G). Since these commutators generate G', the last statement is equivalent to saying that
i.e., that H contains every commutator [x, y], (x, y ∈ G). Since these commutators generate G', the last statement is equivalent to saying that 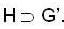 Thus G/H is Abelian if and only if H contains G'.
Thus G/H is Abelian if and only if H contains G'.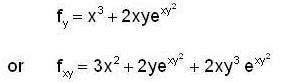 Again,
Again,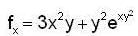
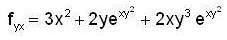
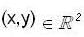 let
let 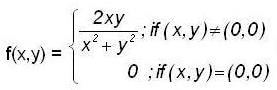 then
then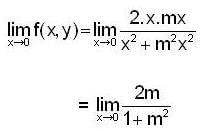
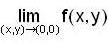 does not exists, therefore f(x,y) is discontinuous at (0,0)
does not exists, therefore f(x,y) is discontinuous at (0,0)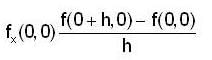
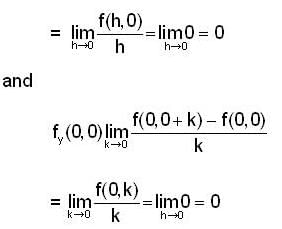
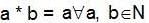
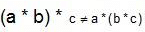
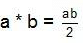 for all a, b ∈ Q. T his is not a group since inverse of element 0 ∈ Q does not exist.
for all a, b ∈ Q. T his is not a group since inverse of element 0 ∈ Q does not exist.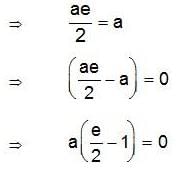
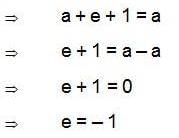
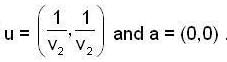
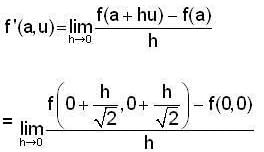


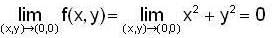 But f(0,0) = 0
But f(0,0) = 0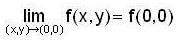
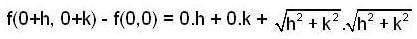 where A = 0, B = 0 which does not depends on h and k and
where A = 0, B = 0 which does not depends on h and k and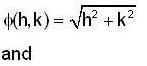
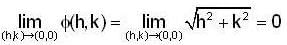 Hence , f(x,y) is continuous as well as differentiable at (0,0).
Hence , f(x,y) is continuous as well as differentiable at (0,0).

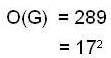
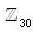 is
is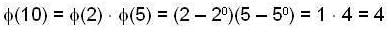
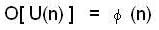
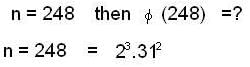
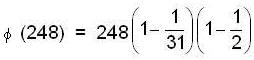
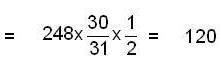
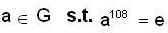
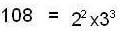
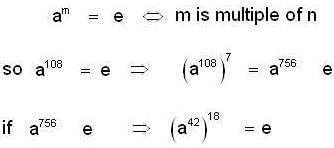
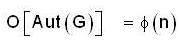
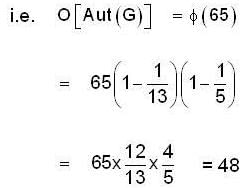
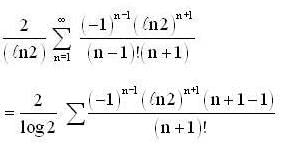
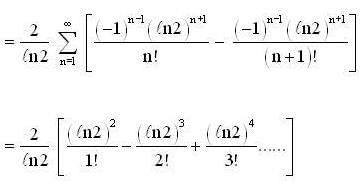
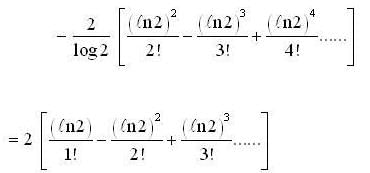
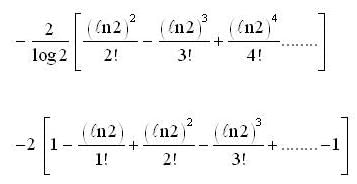
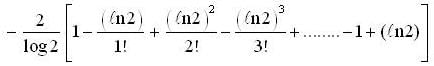
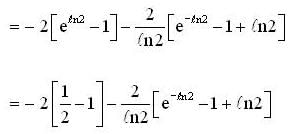
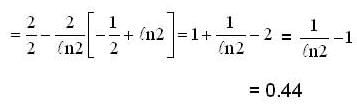
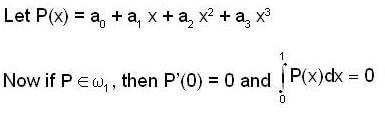
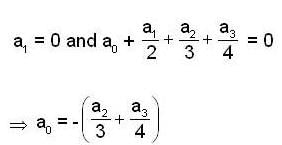

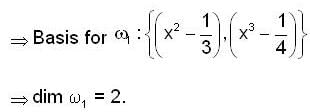
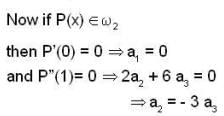
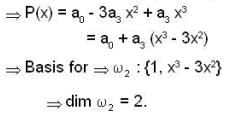
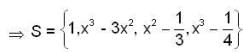
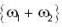 . Now we have to choose L .l. subset of S. and that will be a basis for
. Now we have to choose L .l. subset of S. and that will be a basis for 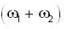 .
.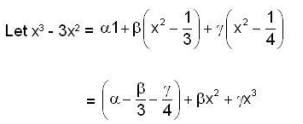
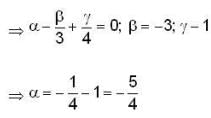
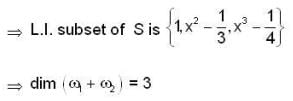

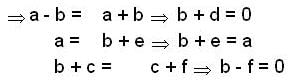
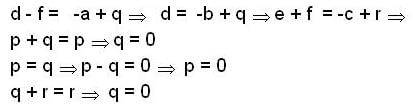
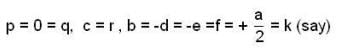
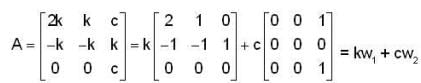
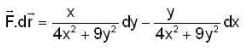
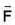 not defined in a region which is enclosed by c so we cannot apply Green's tum here. So we will solve given line integral by definition.
not defined in a region which is enclosed by c so we cannot apply Green's tum here. So we will solve given line integral by definition.