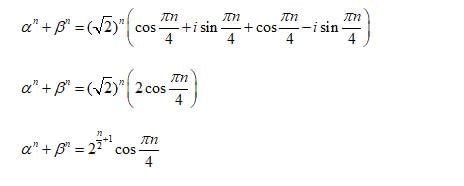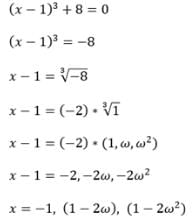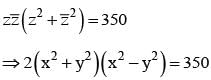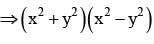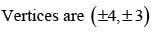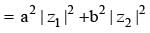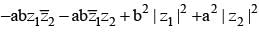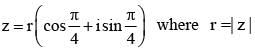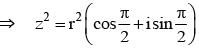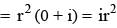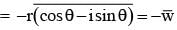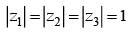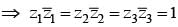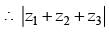JEE Advanced Level Test: Complex Number- 1 - JEE MCQ
30 Questions MCQ Test - JEE Advanced Level Test: Complex Number- 1
The locus of the point z = x + iy satisfying the equation 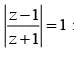 is given by
is given by
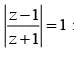 is given by
is given byIf Arg arg[(z−1)/(z+1)] = π/2 then the locus of z is
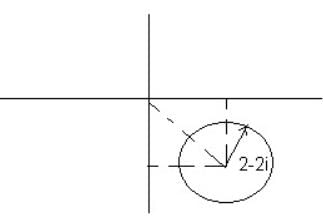
In Argand diagram all the complex numbers z satisfying |z - 4i| + |z + 4i| = 10 lie on a
If z is a complex number, then represents
If w is a complex cube root of unity then the value of (1 + ω) (1 + ω)2 (1 + ω4) (1 + ω8)...2n terms =
If x2 + x + 1 = 0, then the value of 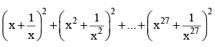 is
is
f |z - 2 + 2i| = 1, then the least value of |z| is
If |z + 2 - i| = 5 and the maximum value of |3z + 9- 7i| is M, then the value of M is ______.
If 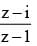 is purely imaginary then the locus of z is
is purely imaginary then the locus of z is
If zr = 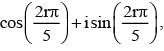 where r = 1,2,3,4,5 then z1z2z3z4z5 =
where r = 1,2,3,4,5 then z1z2z3z4z5 =
For all complex numbers z1z2 such that |z1| = 12 and |z2 - 3 - 4i| = 5 the minimum value of |z1 -z2| is
If a and b are real numbers between 0 and 1 such that the points z1 = a + i, z2 = 1 + bi and z3 =0 form an equilateral triangle then a, b are
If α,β are the roots of x2 - 2x + 4 = 0 then αn + βn =
If the cube roots of unity are 1, ω,ω2 , then the roots of the equation ( x - 1)3 + 8 = 0 are
If |z1| = 2, |z2| = 3, |z3| = 4 and |z1 + z2 + z3| = 5 then |4z2z3 + 9z3z1 + 16z1z2| =
Let z = x + iy be a complex number where x and y are integers then the area of the rectangle whose vertices are the roots of the equation
If z ∈ C and 2z =| z |+i, then z equals
Suppose, a, b, c ∈ C , and | a |=| b |=| c |= 1 and abc = a +b + c, then bc +ca + ab is equal to
The number of complex numbers z which satisfy z2 + 2 | z |2 = 2 is
The complex numbers sin x + i cos 2x and cos x - i sin 2x are conjugate to each other for
If z1 and z2 are two complex numbers are a, b are two real numbers,then |az1 - bz2|2 + |bz1 + az2|2 equals
If z ≠ 0 is a complex number such that arg(z) = π/4,then
Let z and w be two non-zero complex numbers such that |z| = |w| and arg (z) + arg (w) = π. Then z is equal to
If z1, z2, z3 are complex numbers such that
|z1| = |z2| = |z3| =|1/z1 +1/z2 + 1/z3| = 1, then find the value of z1+ z2 + z3 .
If (x + iy)1/3 = a + ib, then x/a + y/b equals


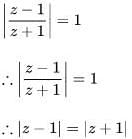

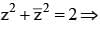
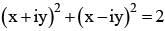
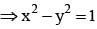
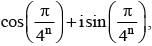 then x1, x2, x3, .....∞
then x1, x2, x3, .....∞
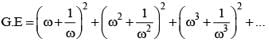 = (1+1+4)9 = 54
= (1+1+4)9 = 54
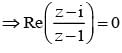
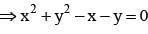
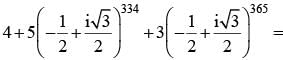
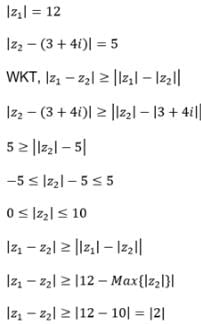
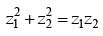 and simplify
and simplify