Airforce X Y / Indian Navy SSR Exam > Airforce X Y / Indian Navy SSR Tests > Mathematics for Airmen Group X > JEE Advanced Level Test: Limits & Derivatives- 1 - Airforce X Y / Indian Navy SSR MCQ
JEE Advanced Level Test: Limits & Derivatives- 1 - Airforce X Y / Indian Navy SSR MCQ
Test Description
30 Questions MCQ Test Mathematics for Airmen Group X - JEE Advanced Level Test: Limits & Derivatives- 1
JEE Advanced Level Test: Limits & Derivatives- 1 for Airforce X Y / Indian Navy SSR 2025 is part of Mathematics for Airmen Group X preparation. The JEE Advanced Level Test: Limits & Derivatives- 1 questions and answers have been
prepared according to the Airforce X Y / Indian Navy SSR exam syllabus.The JEE Advanced Level Test: Limits & Derivatives- 1 MCQs are made for Airforce X Y / Indian Navy SSR 2025 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for JEE Advanced Level Test: Limits & Derivatives- 1 below.
Solutions of JEE Advanced Level Test: Limits & Derivatives- 1 questions in English are available as part of our Mathematics for Airmen Group X for Airforce X Y / Indian Navy SSR & JEE Advanced Level Test: Limits & Derivatives- 1 solutions in
Hindi for Mathematics for Airmen Group X course. Download more important topics, notes, lectures and mock
test series for Airforce X Y / Indian Navy SSR Exam by signing up for free. Attempt JEE Advanced Level Test: Limits & Derivatives- 1 | 30 questions in 60 minutes | Mock test for Airforce X Y / Indian Navy SSR preparation | Free important questions MCQ to study Mathematics for Airmen Group X for Airforce X Y / Indian Navy SSR Exam | Download free PDF with solutions
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 1
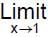 (1 - x + [x - 1] + [1 - x]) is (where [*] denotes greatest integer function)
(1 - x + [x - 1] + [1 - x]) is (where [*] denotes greatest integer function)
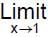 (1 - x + [x - 1] + [1 - x]) is (where [*] denotes greatest integer function)
(1 - x + [x - 1] + [1 - x]) is (where [*] denotes greatest integer function)
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 1
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 4
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 6
 is (where [*] denotes greatest integer function)
is (where [*] denotes greatest integer function)
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 6
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 7
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 10
The 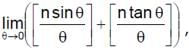 n ∈ N is (where [*] denotes greatest integer function)
n ∈ N is (where [*] denotes greatest integer function)
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 10
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 12
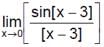 (where [*] denotes greatest integer function)
(where [*] denotes greatest integer function)
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 15
The value of 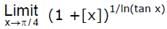 is equal to (where [*] denotes greatest integer function)
is equal to (where [*] denotes greatest integer function)
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 18
If [x] denotes the greatest integer < X , then 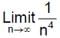 ([13 x] + [23 x] + .....+ [n3 x]) equlas
([13 x] + [23 x] + .....+ [n3 x]) equlas
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 20
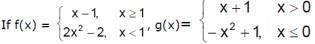 and h(x) = |x| then find
and h(x) = |x| then find  f(g(h(x)))
f(g(h(x)))
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 24
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 26
Given A = 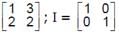 . If A - λ is a singular
. If A - λ is a singular
JEE Advanced Level Test: Limits & Derivatives- 1 - Question 28
Given a real valued function f such that  (where [*] denotes greatest integer function and {*} denotes function part function)
(where [*] denotes greatest integer function and {*} denotes function part function)
Detailed Solution for JEE Advanced Level Test: Limits & Derivatives- 1 - Question 29
|
149 videos|192 docs|197 tests
|
Information about JEE Advanced Level Test: Limits & Derivatives- 1 Page
In this test you can find the Exam questions for JEE Advanced Level Test: Limits & Derivatives- 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for JEE Advanced Level Test: Limits & Derivatives- 1, EduRev gives you an ample number of Online tests for practice
|
149 videos|192 docs|197 tests
|
Download as PDF


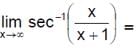
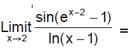

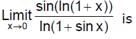
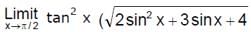
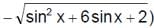 is equal to
is equal to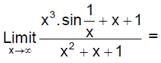

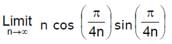 has the value equal to
has the value equal to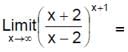
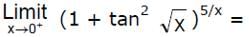

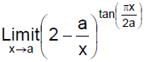 is equal to
is equal to 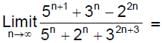
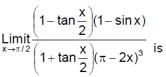
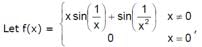 then
then 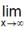 f(x) equals
f(x) equals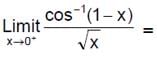
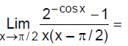
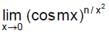
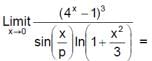
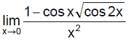 is equal to
is equal to 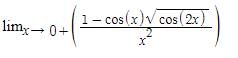

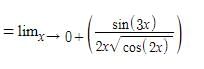
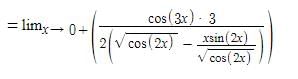
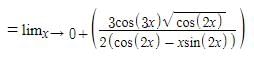
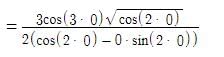
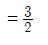
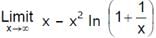 is equal to
is equal to









