KTET Paper 2: Science and Mathematics Test - 5 - KTET MCQ
30 Questions MCQ Test KTET Mock Test Series 2024 - KTET Paper 2: Science and Mathematics Test - 5
The total simple interest for Rs 500 in 8 years and Rs 300 in 16 years is Rs 1100. If the rate of interest is equal in both cases. Then find the rate of interest.
Solve: -60 ÷ [(-4) × (-2) – (-3) × 4]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which of the following is not a component of food?
The additive inverse of S, where S = 1 – 2 + 3 – 4 + 5 – 6 + 7 – 8 + ___ + 49 – 50, is
After vigorous exercise, a person may experience pain in muscles due to
Which of the following statements is correct?
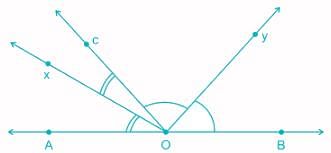
A, O, B are three points on a line segment and C is a points not lying on AOB. If ∠AOC = 40° and OX, OY are the internal and external bisectors of ∠AOC respectively, then ∠BOY is
A tank is 20 m long, 15 m wide and 10 m deep. What is the cost of plastering its walls and bottom at 80 paise per sq. m?
An ammeter has ____________ resistance, so that it passes maximum current through it.
If the area of a trapezium-shaped field is 720 m2, the distance between the two parallel sides is 20 m and the length of one of the parallel sides is 35 m, then the length of the other parallel side is
A factor common to x2 + 7x + 10 and x2 – 3x – 10 is
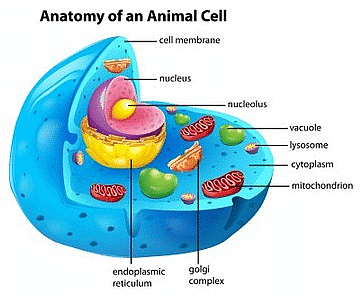
Out of the different combinations of terms given below, the correct combination of terms with reference to an animal cell is
The sum of all the interior angles of a polygon is 1440º. The number of sides of the polygon is
The perimeter of a trapezium is 58 cm and the sum of its non-parallel sides is 20 cm. If its area is 152 cm2, then the distance between the parallel sides, in cm, is
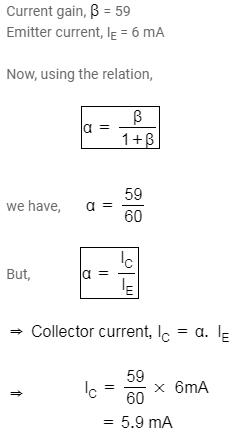
The current gain for a transistor in common emitter configuration is 59. If the emitter current is 6.0 mA, the collector current will be
A box contains some slips on which numbers 25, 26, 27, ..........49, are written (one number in one slip). A slip is drawn at random from the box. What is the probability that the selected slip bears a prime number?
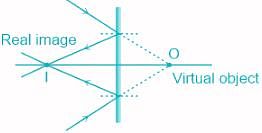
What are the properties of the image formed by the plane mirror?
A. Virtual and inverted
B. Virtual and erect
The length of a rectangular field is twice its breadth. If the area of the field is 288 sq.m., the length of the field is:
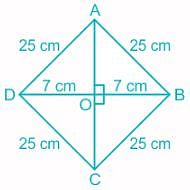
The perimeter of a rhombus is 100 cm and the length of its smaller diagonal is 14 cm. Find the area of the rhombus?
Which of the following is incorrect about summative assessments?
Which one of the following is the most suited to the development of scientific skills in students?
A teacher asked the students to find the number of possible pentominoes using five squares and then further explore the number of possible hexominoes and so on. These types of activities help the child to
A student verifies the outcome when two fractions are multiplied together. This specification belongs to the objective of
A teacher before beginning to teach 'Digestion' to class VI students provides them with the outline diagram of a human body and asks them to draw all parts, through which they think the food would travel from mouth when they eat.
What could be the teacher's purpose of asking this question?
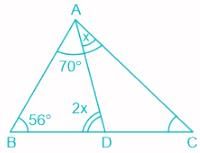
In ΔABC, D is a point on BC such that ∠ADB = 2∠DAC, ∠BAC = 70° and ∠B = 56°. What is the measure of ∠ADC?
Individual attention can not be paid to student due to:
Which of the following is not the process by which children learn?
1. Simulation
2. Observation
Choose the correct code
To find the median of the continuous series, we use the formula; Median = 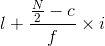 . What does 'C' here denote?
. What does 'C' here denote?
When upper grade children do research work, the major problem the teacher has to contend with is
|
100 tests
|