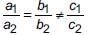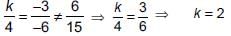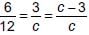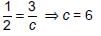Math Olympiad Test: Linear Equations in Two Variables- 3 - Class 10 MCQ
10 Questions MCQ Test - Math Olympiad Test: Linear Equations in Two Variables- 3
The sum of the digits of a two-digit number is 12. The number obtained by interchanging the two digits exceeds the given number by 18. Find the number.
The sum of two numbers is 8 and the sum of their reciprocals is 8/15. Find the numbers.
If am = bl and bn ≠ cm, then the system of equations
ax + by = c
lx + my = n
ax + by = c
lx + my = n
The denominator of a rational number is greater than its numerator by 3. If 3 is subtracted from the numerator and 2 is added to the denominator, the new number becomes 1/5. Then the original number was _______.
If the system of equations
2x + 3y = 7
2ax + (a + b)y = 28
has infinitely many solutions, then the values of a and b respectively are _______.
The value of k, for which the system of equations kx – 3y + 6 = 0, 4x – 6y + 15 = 0 represent parallel lines, is _______.
ax + by + c = 0 does not represent an equation of line when _______.
In a ΔABC, ∠C = 3 ∠B = 2 (∠A + ∠B). The three angles will be _______.
How many values of c, for which the system of equations 6x + 3y = c – 3, 12x + cy = c has infinitely many solutions?
The ratio of a 2-digit number to the sum of digits of that number is 4 : 1. If the digit in the unit place is 3 more than the digit in the tens place, what is the number?


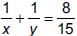 ...(2)
...(2)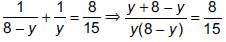

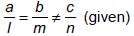
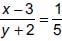 ⇒ 5x – 15 = y + 2
⇒ 5x – 15 = y + 2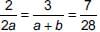
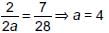 ...(2)
...(2)