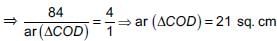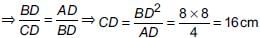Class 10 Exam > Class 10 Tests > Math Olympiad Test: Triangles - 3 - Class 10 MCQ
Math Olympiad Test: Triangles - 3 - Class 10 MCQ
Test Description
10 Questions MCQ Test - Math Olympiad Test: Triangles - 3
Math Olympiad Test: Triangles - 3 for Class 10 2025 is part of Class 10 preparation. The Math Olympiad Test: Triangles - 3 questions and answers have been prepared
according to the Class 10 exam syllabus.The Math Olympiad Test: Triangles - 3 MCQs are made for Class 10 2025 Exam.
Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Math Olympiad Test: Triangles - 3 below.
Solutions of Math Olympiad Test: Triangles - 3 questions in English are available as part of our course for Class 10 & Math Olympiad Test: Triangles - 3 solutions in
Hindi for Class 10 course.
Download more important topics, notes, lectures and mock test series for Class 10 Exam by signing up for free. Attempt Math Olympiad Test: Triangles - 3 | 10 questions in 10 minutes | Mock test for Class 10 preparation | Free important questions MCQ to study for Class 10 Exam | Download free PDF with solutions
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 1
Math Olympiad Test: Triangles - 3 - Question 2
In the given figure, DABC ~ DDCB, then AB × DB =
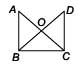

Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 2
Math Olympiad Test: Triangles - 3 - Question 3
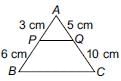
P and Q are points on sides AB and AC respectively of ΔABC. If AP = 3 cm, PB = 6 cm, AQ = 5 cm and QC = 10 cm, then BC =
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 3
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 4
Math Olympiad Test: Triangles - 3 - Question 5
ABC is right triangle, right angled at C. If p is the length of the perpendicular from C to AB and a, b, c have the usual meaning, then 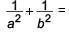
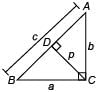
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 5
Math Olympiad Test: Triangles - 3 - Question 6
In the given figure, AD ⊥ BC, BE ⊥ AC, CF ⊥ AB, then AF2 + BD2 + CE2 =
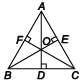
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 6
Math Olympiad Test: Triangles - 3 - Question 7
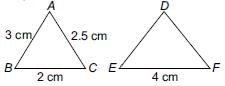
ΔABC is such that AB = 3 cm, BC = 2 cm and CA = 2.5 cm. If ΔDEF ~ ΔABC and EF = 4 cm, then perimeter of ΔDEF is
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 7
Math Olympiad Test: Triangles - 3 - Question 8
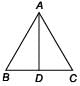
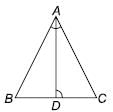
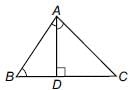
In the given ΔABC, AD⊥BC and ∠A is right angled. Then AD2 =
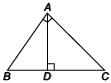
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 8
Math Olympiad Test: Triangles - 3 - Question 9
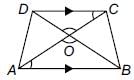
In the given trapezium ABCD, AB || CD and AB = 2CD. If area of ΔAOB = 84 cm2, then the area of ΔCOD is
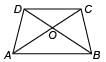
Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 9
Math Olympiad Test: Triangles - 3 - Question 10
In the given figure, ∠ ABC = 90° and BD ⊥ AC . If BD = 8 cm, AD = 4 cm, then CD =

Detailed Solution for Math Olympiad Test: Triangles - 3 - Question 10
Information about Math Olympiad Test: Triangles - 3 Page
In this test you can find the Exam questions for Math Olympiad Test: Triangles - 3 solved & explained in the simplest way possible.
Besides giving Questions and answers for Math Olympiad Test: Triangles - 3, EduRev gives you an ample number of Online tests for practice
Download as PDF




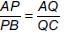
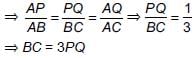
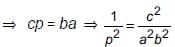
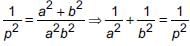
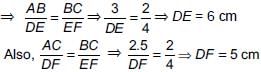

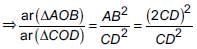 [∵ AB = 2CD]
[∵ AB = 2CD]