Mathematical Statistics - 2014 Past Year Paper - IIT JAM MCQ

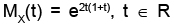
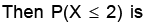
A system consisting of n components functions if, and only if, at least one of n components functions. Suppose that all the n components of the system function independently, each with probability 3/4. If the probability of functioning of the system is 63/64, then the value of n is

The matrix

Let the mappings T₁, T₂, T₃, T₄ from R³ to R³ to be defined by

T₁(x, y, z) = (x² + y², x + z, x + y + z);
T₁(x, y, z) = (y + z, z + x, x + y);
T₁(x, y, z) = (x + y, xy, x – z);
T₄(x, y, z) = (x, 2y, 3z);

Then which of these are linear transformations of R³ over R ?

Let

Then the matrix of the linear transformation T : R³ → R³ defined by T(X) = TX; with respect to the basis

Let X₁, X₂, X₃ and X₄ be independent random variables. Then which of the following pairs of random variables are independent ?

The series

Let X be a random variable of continuous type with probability density function

Based on single observation X, the most powerful; test of size α = 0.1, for testing H₀ : θ = 1 against H₁ : q = 2, rejects H₀ if X < k. Then the value of k is

Let X be a random variable of continuous type with probability density function f(x). Then, based on single observation X, the most powerful test of size α = 0.1 for testing H₀ : f(X) = 2x, 0 < x < 1, against H₁ : f(X) = 4x², 0 < x < 1, has power

Let X and Y be two random variables of discrete type with respective probability mass functions as

Let X and Y denote the lifetimes (in years) of two independent component in a series with respective probability density functions

Then the probability that the system will survive for at least 21 years, is

The distribution function of a random variable X is given by

Four persons P, Q, R and S take turns (in the sequence P, Q, R, S, P, Q, R, S, P, ...) in rolling a fair die. The first person to get a six wins. Then the probability that S wins is

The function

has

The area of the region bounded by y = 8 and y = |x² – 1|, is

Let X₁, X₂, ... be a sequence of i.i.d. U[0, 1] random variables.

Let X = (X₁, X₂) have a bivariate normal distribution with 

There are two urns U₁ and U₂, U₁ contains four white and four black balls, and U₂ is empty. Four balls are drawn at random from U₁ and transferred to U₂. Then a ball is drawn at random from U₂. The probability that the ball drawn from U₂ is white is

The integral

is equal to

In which cases the system of equations

x₁ – 2x₂ + x₃ = 3
2x₁ – 5x₂ + 2x₃ = 2
x₁ + 2x₂ + λx₃ = μ

Which of the following differential equations is satisfied by functions  and y₂(x) = e^–2x?

Let

Then

Let {a_n} be a sequence of positive real numbers such thatThen the function

is

Find the mean of x + 77, x + 7, x + 5, x + 3 and x – 2?

The number of distinct eigenvalues of the matrix

is

Let X₁, X₂, ... be i.i.d. random variables with common probability density function

Define  If

Let X₁, ..., X_n (n > 2) be a random sample from a population with probability density function

Then a uniformly minimum variance unbiased estimator of θ is

Let X = (X₁, X₂) have joint probability density function

Then the variance of random variable X₁ is