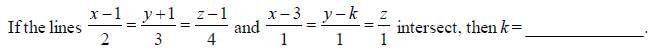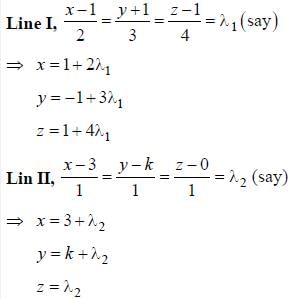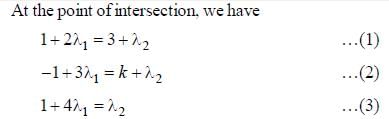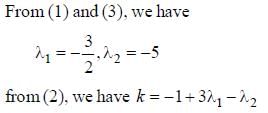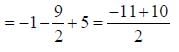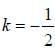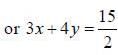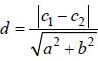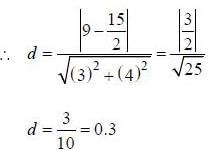Mathematics MCQ 1 - Biotechnology Engineering (BT) MCQ
21 Questions MCQ Test - Mathematics MCQ 1
If Z is a complex number, then the minimum value of |z| + |z-l| is
The product of all real roots of the equation x2 - |x| - 6 = 0 is
Two dice are rolled simultaneously. The probability that the sum of the two numbers on the top faces will be at least 10 is
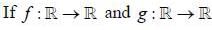 are defined by f(x) = 2x + 3 and g (x) = x2 + 7, Then the value of x such that g (f(x)) = 8 are
are defined by f(x) = 2x + 3 and g (x) = x2 + 7, Then the value of x such that g (f(x)) = 8 are
Let R = {(3,3),(6.6),(9,9),(12,12),(6.12),(3,9),(3,12),(3,6)} be a relation on the se A = {3,6,9,12}. The relation is
In throwing a die, let
A be the event 'coining up of an odd number'
B be the event 'coming up of an even number'
C' be the event ‘coming up of a number > 4' and D be the event ‘coming up of a number <3'
Then
The diffemetial equation representing the family of curves. y2 = 2c (x + √c). where c is positive parameter is of
The equations of lines which pass through the point (3, -2) and are inclined at 60° to the line 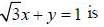
The number of arrangements of the letters of the word BANANA in which the two N’s do not appear adjacently is _____________.
On the interval [0,1], the function f(x) = x25 (1 - x)75 takes its maximum value at the point _______.
If E = {1,2,3,4} and F = {1,2}, then the niunber of onto functions on E to F is ______.
The distance between the lines 3x + 4y = 9 and 6x + 8y = 15 is _______.


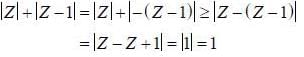
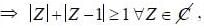

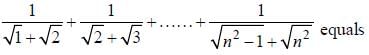
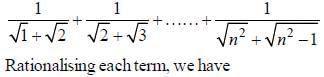
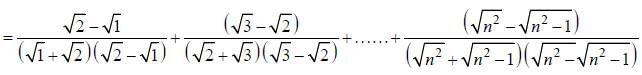
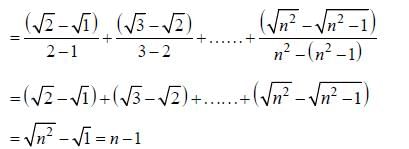
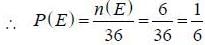
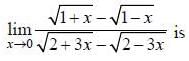
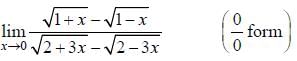
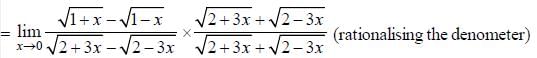
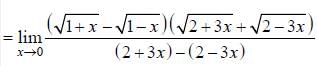
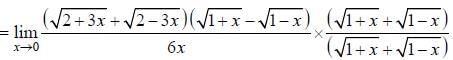
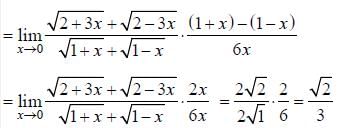
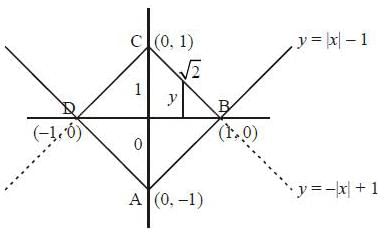
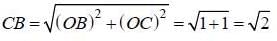
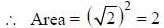
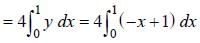 (as equation of CB is y = -x+ 1)
(as equation of CB is y = -x+ 1)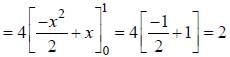
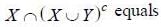
 (using De'morgans law)
(using De'morgans law) 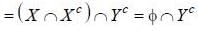
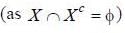
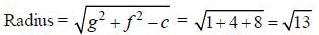
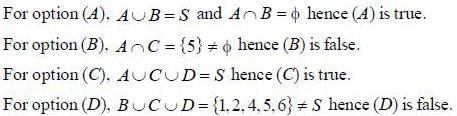
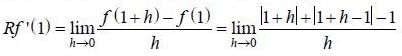
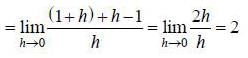
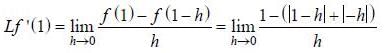

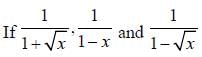 are consecutive forms of a series, then series is
are consecutive forms of a series, then series is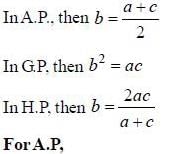
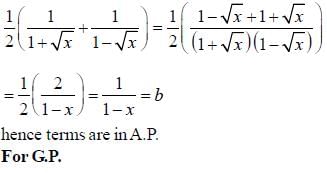
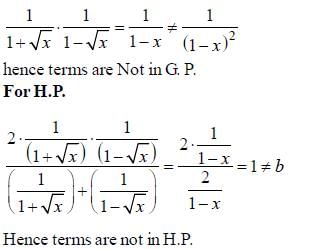
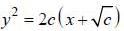 ......(1)
......(1)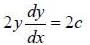
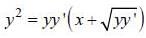


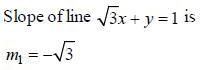
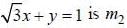
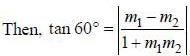
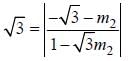
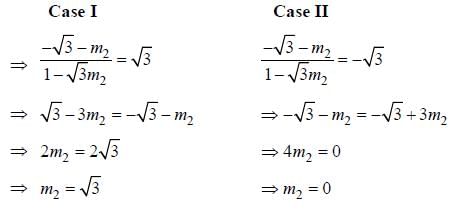
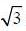 and the otehr one is having slope 0.
and the otehr one is having slope 0. 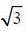

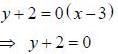
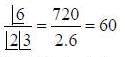


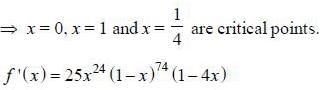
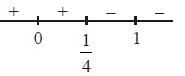
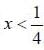 and f (x) is decreasing when
and f (x) is decreasing when