Mathematics Mock Test - 8 - CDS MCQ
30 Questions MCQ Test CDS (Combined Defence Services) Mock Test Series 2024 - Mathematics Mock Test - 8
Let S be the set of prime numbers greater than or equal to 2 and less than 100. Multiply all the elements of S. With how many consecutive zeroes will the product end?
The integers 34041 and 32506 when divided by a three-digit integer n leave the same remainder. What is n?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The number of girls appearing for an admission test is twice the number of boys. If 30% of the girls and 45% of the boys get admission, the percentage of candidates who do not get admission is
Meena scores 40% in an examination and after review, even though her score is increased by 50%, she fails by 35 marks. If her post-review score is increased by 20%, she will have 7 marks more than the passing score. The percentage score needed for passing the examination is
The average of 15 numbers is 18. If each number is multiplied by 9, then the average of the new set of numbers is:
The average weight of 3 boys Ross, Joey and Chandler is 74 kg. Another boy David joins the group and the average now becomes 70 kg. If another boy Eric, whose weight is 3 kg more than that of David, replaces Ross then the average weight of Joey, Chandler, David and Eric becomes 75 kg. The weight of Ross is:
In a library, the ratio of number of story books to that of non-story books was 4:3 and total number of story books was 1248. When some more story books were bought, the ratio became 5:3. Find the number of story books bought.
If A and B together can complete a piece of work in 15 days and B alone in 20 days, in how many days can A alone complete the work?
Two cars started simultaneously towards each other and met each other 3 h 20 min later. How much time will it take the slower car to cover the whole distance if the first arrived at the place of departure of the second 5 hours later than the second arrived at the point of departure of the first?
One root of the quadratic equation x2 - 12x + a = 0, is thrice the other. Find the value of a?
The number of integers n that satisfy the inequalities | n - 60| < n - 100| < |n - 20| is
If 2 ≤ |x – 1| × |y + 3| ≤ 5 and both x and y are negative integers, find the number of possible combinations of x and y.
If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:
If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:
The H.C.F. of two numbers is 23 and the other two factors of their L.C.M. are 13 and 14. The larger of the two numbers is:
A feeding bottle is sold for Rs. 150. Sales tax accounts for one-fifth of this and profit one-third of the remainder. Find the cost price of the feeding bottle.
A man sells an article at 10% above its cost price. If he had bought it at 15% less than what he paid for it and sold it for Rs. 33 less, he would have gained 10%. Find the cost price of the article.
A sum of money at simple interest amounts to Rs. 815 in 3 years and to Rs. 854 in 4 years. The sum is :
A sum of money amounts to Rs.9800 after 5 years and Rs.12005 after 8 years at the same rate of simple interest. The rate of interest per annum is
A randomly selected year is containing 53 Mondays then probability that it is a leap year
A bag contains 4 black, 5 yellow and 6 green balls. Three balls are drawn at random from the bag. What is the probability that all of them are yellow?
Two trains having equal lengths, take 10 seconds and 15 seconds respectively to cross a post. If the length of each train is 120 meters, in what time (in seconds) will they cross each other when traveling in opposite direction?
Find the quadratic equations whose roots are the reciprocals of the roots of 2x2 + 5x + 3 = 0?
I. a2 + 8a + 16 = 0,
II. b2 - 4b + 3 = 0 to solve both the equations to find the values of a and b?
|
23 docs|73 tests
|
|
23 docs|73 tests
|


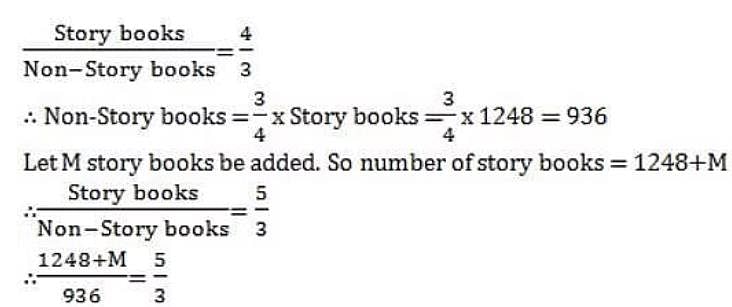
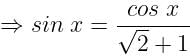
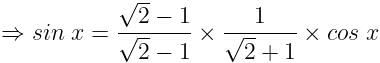

 Principal = Rs. (815 - 117) = Rs. 698.
Principal = Rs. (815 - 117) = Rs. 698.















