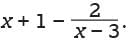Mathematics Test - 4 - SAT MCQ
30 Questions MCQ Test Digital SAT Mock Test Series 2024 - Mathematics Test - 4
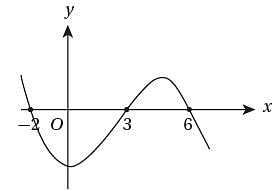
If m > 1, which of the following could be the graph of y = -(x + m)2 + m in the xy-plane?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In the figure above, triangle ABC has an area of 19. What is the value of tan θ?

In the figure above, triangle ABC has an area of 19. What is the value of tan θ?
The average (arithmetic mean) of a set of 3 positive integers is m. If the number 24 is added to this set, what is the average (arithmetic mean) of the new set of numbers?
Question based on the graph below
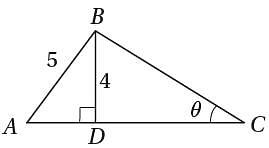
Q. A university surveyed 24 economics majors and asked them how many credits they received the previous semester. The results are represented in the graph above. What percentage of these students received 15 or more credits that semester?
If i = √-1, which of t he follow ing is equivalent to (2 - i)(3 - 2i) ?
After its initial offering, the price of a stock increased by 20% in the first year, decreased by 25% in the second year, then increased by 10% in the third year. What was the net change in the stock price over the entire three-year period?
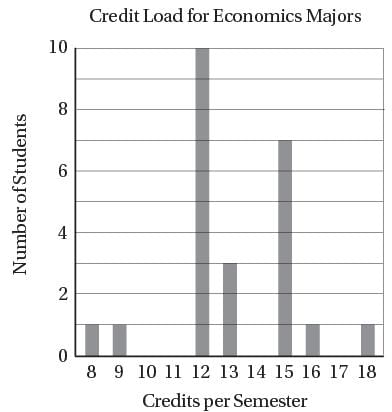
A rectangular solid above has dimensions 3, a, and b, where a and b are integers. Which of the following CANNOT be the areas of three different faces of this solid?
The function g(x) = ax3 + bx2 + cx + d has zeroes at x = -2 , x = 3, and x = 6. If g(0) < 0, which of the following must also be negative?
Question based on the graph below.

Which of the following statements is most directly justified by the data shown in the scatterplot above?
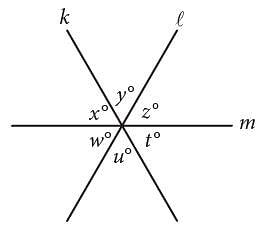
In the figure above, lines k, ℓ, and m intersect at a point. If x + y = u + w, which of the following must be true?
I. x = z
II. y = w
III. z = t
x3(x2 − 5) = − 4x
If x > 0, what is one possible solution to the equation above?
Question refer to the following information.
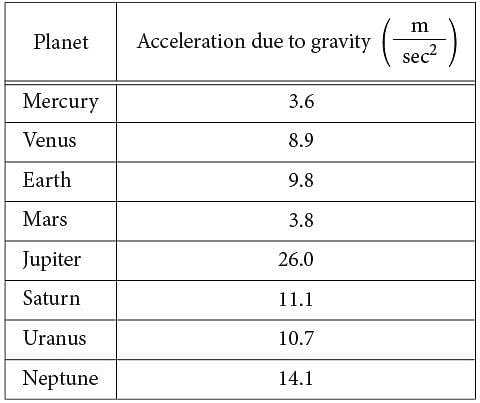
The chart above shows approximations of the acceleration due to gravity in meters per second squared  for the eight planets in our solar system. The weight of an object on a given planet can be found by using the formula W =mg , where W is the weight of the object measured in newtons, m is the mass of the object measured in kilograms, and g is the acceleration due to gravity on the planet measured in m/sec2.
for the eight planets in our solar system. The weight of an object on a given planet can be found by using the formula W =mg , where W is the weight of the object measured in newtons, m is the mass of the object measured in kilograms, and g is the acceleration due to gravity on the planet measured in m/sec2.
Q. An object on Earth has a weight of 150 newtons. On which planet would the same object have an approximate weight of 170 newtons?

Graphs of the functions f and g are shown in the xy-plane above. For which of the following values of x does f(x) + g(x) = 0 ?
Of the following four types of savings account plans, which option would yield exponential growth of the money in the account?
2(p + 1) + 8(p − 1) = 5p
What value of p is the solution of the equation above?
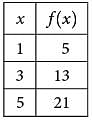
Some values of the linear function f are shown in the table above. Which of the following defines f?
The Downtown Business Association (DBA) in a certain city plans to increase its membership by a total of n businesses per year. There were b businesses in the DBA at the beginning of this year. Which function best models the total number of businesses, y, the DBA plans to have as members x years from now?

The system of equations above has solution (x, y). What is the value of x?
Question refer to the following information.

One method of calculating the approximate age, in years, of a tree of a particular species is to multiply the diameter of the tree, in inches, by a constant called the growth factor for that species. The table above gives the growth factors for eight species of trees.
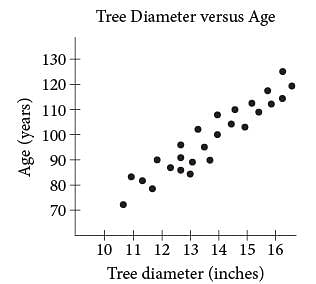
The scatterplot above gives the tree diameter plotted against age for 26 trees of a single species. The growth factor of this species is closest to that of which of the following species of tree?
Ken is working this summer as part of a crew on a farm. He earned $8 per hour for the first 10 hours he worked this week. Because of his performance, his crew leader raised his salary to $10 per hour for the rest of the week. Ken saves 90% of his earnings from each week. What is the least number of hours he must work the rest of the week to save at least $270 for the week?
The number of radians in a 720-degree angle can be written as απ , where a is a constant. What is the value of α?
A certain package requires 3 centimeters of tape to be closed securely. What is the maximum number of packages of this type that can be secured with 6 meters of tape? (1 meter = 100 cm)
Question refer to the following information.
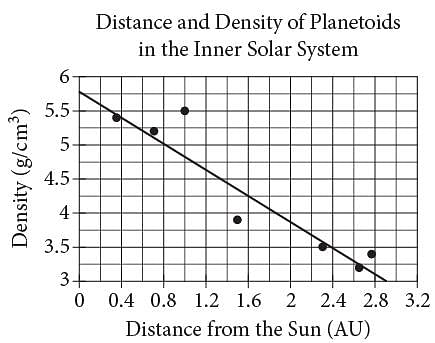
The scatterplot above shows the densities of 7 planetoids, in grams per cubic centimeter, with respect to their average distances from the Sun in astronomical units (AU). The line of best fit is also shown.
Q. An astronomer has discovered a new planetoid about 1.2 AU from the Sun. According to the line of best fit, which of the following best approximates the density of the planetoid, in grams per cubic centimeter?
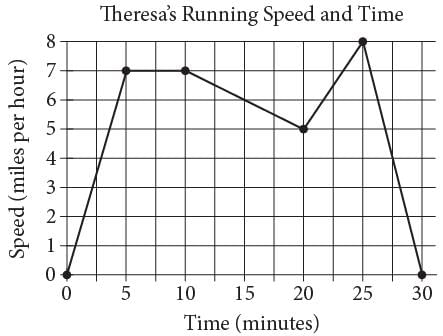
Theresa ran on a treadmill for thirty minutes, and her time and speed are shown on the graph above.
According to the graph, which of the following statements is NOT true concerning Theresa’s run?
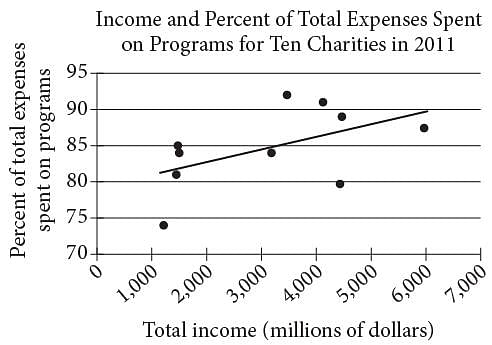
The scatterplot above shows data for ten charities along with the line of best fit. For the charity with the greatest percent of total expenses spent on programs, which of the following is closest to the difference of the actual percent and the percent predicted by the line of best fit?
|
8 docs|15 tests
|


 where m > 0, what is t he least possible value of m ?
where m > 0, what is t he least possible value of m ?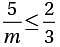
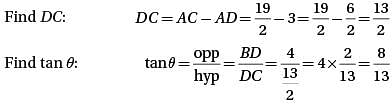 or .615
or .615

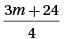
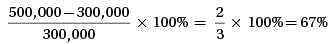
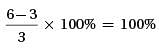
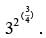 Applying the properties of exponents, this can be written as 33/2, which can further be rewritten as 32/2(31/2), an expression that is equivalent to 3√3.
Applying the properties of exponents, this can be written as 33/2, which can further be rewritten as 32/2(31/2), an expression that is equivalent to 3√3. 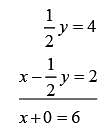
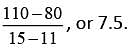 The slope of the equation is interpreted as the growth factor for a species of tree. According to the table, the species of tree with a growth factor of 7.5 is shagbark hickory.
The slope of the equation is interpreted as the growth factor for a species of tree. According to the table, the species of tree with a growth factor of 7.5 is shagbark hickory.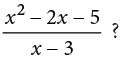
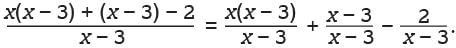 . Since the given expression is defined for x ≠ 3, the expression can be rewritten as
. Since the given expression is defined for x ≠ 3, the expression can be rewritten as