Model Test Paper, Math, Feb. - 2017 - IIT JAM MCQ
30 Questions MCQ Test IIT JAM Past Year Papers and Model Test Paper (All Branches) - Model Test Paper, Math, Feb. - 2017
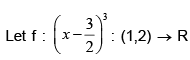 is differentiable, then f is strictly increasing on the interval
is differentiable, then f is strictly increasing on the interval
Let f : [a, b] → R be a differentiable function s.t. f(x) ≠ 0 for x ∈ [a, b] then  is equal to
is equal to
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The area of the region that is inside the circle r = 2 cos q and outside the cardiod r = 2(1 – cos q).
Fg and Fe represents gravitational and electrostatic forces respectively, between the two electrons situated at a distance of 10 m. The ratio Fg/Fe is of the order of
Consider the funnel formed by revolving the curve y = 1/x about the x- axis, between x = 1 and x = a, where a > 1 If Sa denote the surface area of the funnel then
Let x ∈ R, n ∈ N then there exist a unique y ∈ R s.t. yn = x if
If both f, g : R → R are discontinuous at 0, then the product function fg : R → R is
Let A be a n × n matrix and y be a n × 1 matrix (vector) such that the equation Ax = y for a n × 1 matrix (vector) y admits no solution then the rank of A is
Let b be an n × 1 (column) vector and A be an n × n positive definite matrix. Define P : Rn → R by
Here t stands for transpose. If x0 is a vector such that Ax0 = B then which of the following is true? (where t is used for transpose)
U = {(x, y, z) | x = y = z}, V = {(x, y, z) | x = 0} what is U + V?
Let A, B ⊂ Rn and define, A + B = {a + b; a ∈ A, b ∈ B}. If A and B are open then which of the following statement is TRUE ?
The value of the integral where R is the following solid region
Let S be the surface in R3 defined by the parametric equation
r = 2 + cos t + cos u
θ = t 0 ≤ t ≤ 2π
z = sin u 0 ≤ u ≤ 2π
then the using the divergence theorem what is the volume of the region inside S.
The following picture shows the parametric curve (x, y) = (t – t3, t2)
By using Green’s theorem what will be the area of the shaded region.
Let G be a finite group of order 2n for some integer n. Consider the map Ø : G → G given by Ø(a) = a2. Then which of the following statement holds?
If F is a conservative vector field where then what should be the value of λ
A rigid body is rotating with constant angular velocity ω about fixed axis. If V be the velocity at any point of the body then the value of curl V will be
An ideal gas has molecules with 5 degrees of freedom. The ratio of specific heats at constant pressure (Cp ) and at constant volume (Cv ) is :
For what values of λ and μ the system of equations
2x + 3y + 5z = 9
7x + 3y – 2z = 8
2x + 3y + λz = μ
has unique solution
Which of the following mapping is not linear ?
The value of y as t → ∞ for an initial value of y(1) = 0, for the differential equation
If y1 = sinx and y2 = sinx – cosx are linearly independent solutions of y” + y = 0. Then determine the constants c1 and c2 so that the solution sin x + 3cosx = c1y1 + c2y2.
General solution of the differential equation
Let u1, ... un be a linearly dependent set of functions on a ≤ x ≤ b, and let each function be(n – 1) times differentiable in (a, b). Then
|
29 docs|48 tests
|
|
29 docs|48 tests
|

















