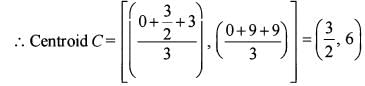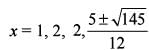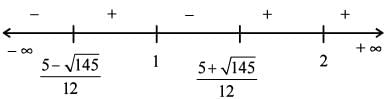NDA I - Mathematics Question Paper 2016 - Defence MCQ
30 Questions MCQ Test - NDA I - Mathematics Question Paper 2016
Suppose ω is a cube root of unity with ω≠1. Suppose P and Q are the points on the complex plane defined by ω and ω2. If O is the origin, then what is the angle between OP and OQ?
Suppose there is a relation * between the positive numbers x and y given by x * y if and only if x ≤ y2. Then which one of the following is correct?
If x2+ px + 4 for all real values of x, then which one of thefollowing is correct?
If z=x + iy= 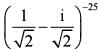 , where i = √-1, then what is the fundamental amplitude of
, where i = √-1, then what is the fundamental amplitude of 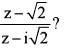
If f(x1)- f(x2) is 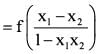 for x1, x2 ∈ (-1,1), then what is f(x) equal to?
for x1, x2 ∈ (-1,1), then what is f(x) equal to?
What is the range of the function 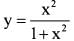 2 ,where X ∈R?
2 ,where X ∈R?
A straight line intersects x and y axes at P and Q respectively If (3,5) is the middle point of PQ, then what is the area ofthe triangle OPQ?
If a circle of radius b units with centre at (0, b) touches the line y = x — a√2 , then what is the value of b?
Consider the function f(θ)= 4(sin2 θ+ cos4 θ)
Q. What is the maximum value of the function f(θ)?
Consider the function f(θ)= 4(sin2 θ+ cos4 θ)
Q. What is the minimum value of the function f(θ)?
Consider the function f(θ)= 4(sin2 θ+ cos4 θ)
Consider the following statements:
f(θ) = 2 has no solution.
f(θ) = 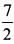 has a solution.
has a solution.
Q. Which of the above statements is/are correct?
Consider the function 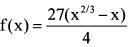
How many solutions does the function f(x) = 1 have?
Consider the function 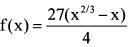
How many solutions does the function f(x) = -1 have?
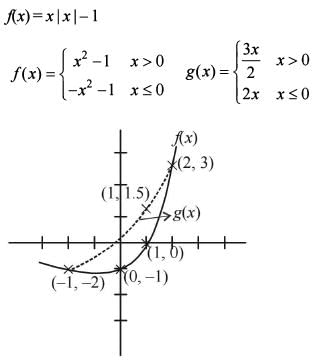
Consider the functions
f(x) = xg(x) and g(x = 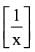
Where [•] is the greatest integer function.
What is 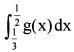 equal to?
equal to?
Consider the function f ( x ) = | x - 1 |+ x2 , w here x ∈R .
Which one of the following statements is correct?
Consider the function f ( x ) = | x - 1 |+ x2 , w here x ∈R .
Which one of the following statements is correct?
Which one of the following statements is correct?
What is the area of the region bounded by x-axis, the curve y = f(x) and the two ordinates 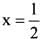 and x = 1 ?
and x = 1 ?
What is the area of the region bounded by x-axis, the curve y = f(x) and the two ordinates x = 1 and 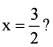
Given that an = 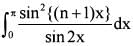
Consider the following statements:
1. The sequence {a2n} is in AP with common difference zero.
2. The sequence {a2n+1} is in AP with common difference zero.
Which of the above statements is/are correct?
Given that an = 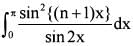
What is an-1 - an-4 equal to ?
Consider the equation x + |y| = 2y.
Which of the following statements are not correct?
1. y as a function of x is not defined for all real x.
2. y as a function of x is not continuous at x = 0.
3. y as a function of x is differentiable for all x.
Q. Select the correct answer using the code given below.
Consider the equation x + |y| = 2y.
What is the derivative of y as a function of x with respect to x for x < 0?
Consider the lines y = 3x, y = 6x and y = 9
What is the area of the triangle formed by these lines?
Consider the lines y = 3x, y = 6x and y = 9
The centroid of the triangle is at which one of the following points?
Consider the function f(x) = (x - l )2 ( x + 1) (x - 2)3
Q. What is the number of points of local minima of the function f(x)?
Consider the function f(x) = (x - l )2 ( x + 1) (x - 2)3
What is the number of points of local maxima of the function f(x) ?


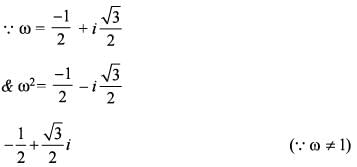
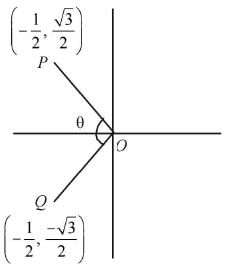
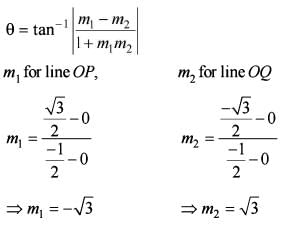
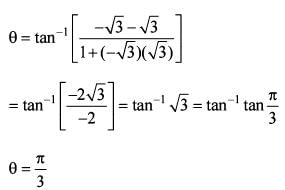

 positive numbers.
positive numbers.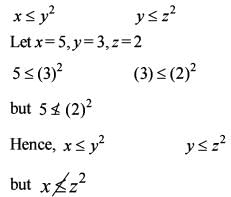
 (I)2
(I)2 positive numbers is reflexive, but not transitive and symmetric.
positive numbers is reflexive, but not transitive and symmetric.
 real values of x.
real values of x.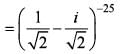
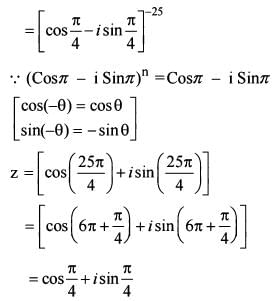
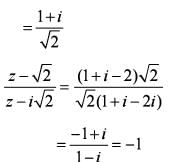
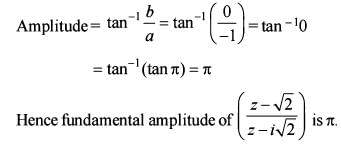
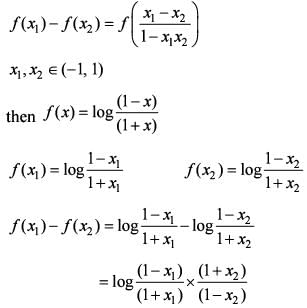
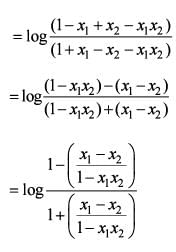
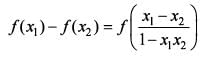
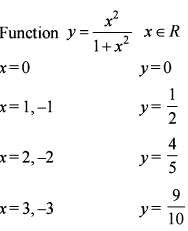

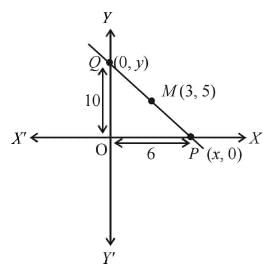 ∵ M is the mid point of PQ
∵ M is the mid point of PQ
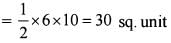

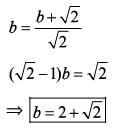
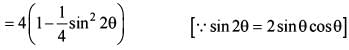
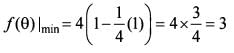
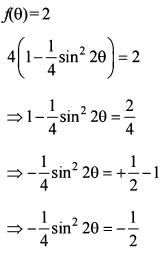
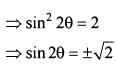
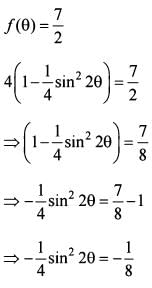
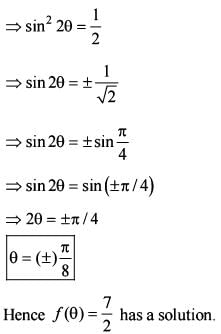
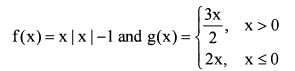
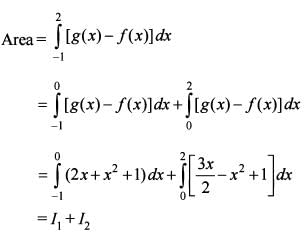

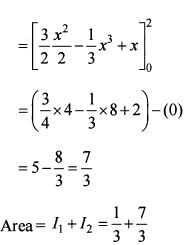
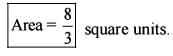
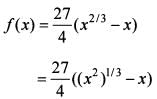
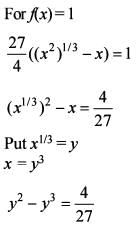
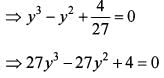
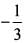 then ( 3y + 1) = 0 is a factor o f cubic equation.
then ( 3y + 1) = 0 is a factor o f cubic equation.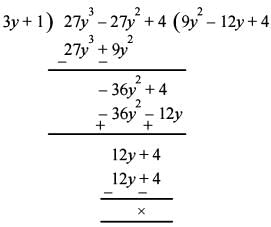
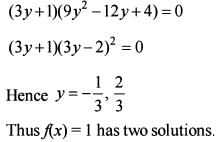
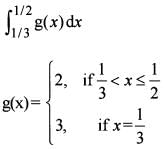
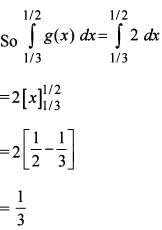
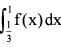 equal to ?
equal to ?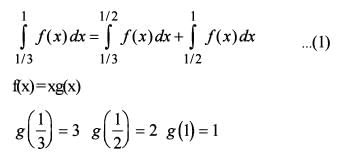
 will be 2 and in range
will be 2 and in range
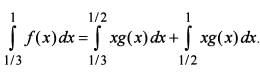
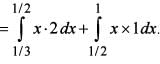
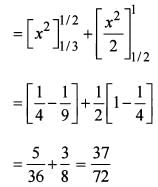
 x ∈R
x ∈R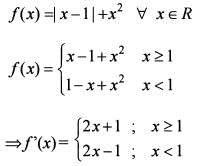
 and increasing
and increasing 
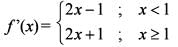
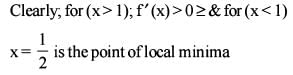
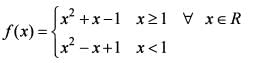
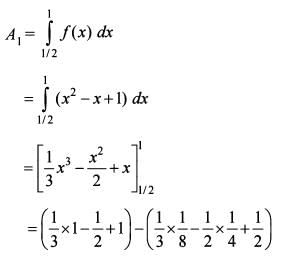
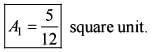
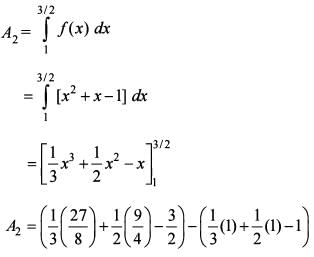
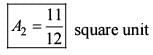
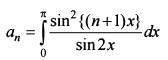


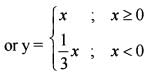
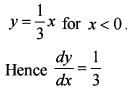

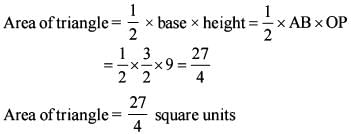
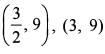 respectively.
respectively.