Probability (Easy Level) - CAT MCQ
12 Questions MCQ Test Quantitative Aptitude (Quant) - Probability (Easy Level)
What is the chance of throwing a number greater than 4 with an ordinary dice whose faces are numbered from 1 to 6?
Find the chance of drawing 2 blue balls in succession from a bag containing 5 red and 7 blue balls, if the balls are not being replaced.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
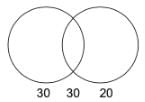
100 students appeared for two examinations. 60 passed the first, 50 passed the second and 30 passed both. Find the probability that a student selected at random has failed in both the examinations?
In rolling two dices, find the probability that there is at least one ‘6’
From a bag containing 4 white and 5 black balls a man draws 3 at random. What are the odds against these being all black?
Phoebe throws three dice in a special game of Ludo. If it is known that he needs 15 or higher in this throw to win then find the chance of his winning the game
Find out the probability of forming 187 or 215 with the digits 1, 2, 3, 4, 5, 6, 7, 8, 9 when only numbers of three digits are formed and when repetitions are not allowed.
Two fair dice are thrown. What is the probability that the sum is less than 10?
In a certain lottery the prize is ` 1 crore and 5000 tickets have been sold. What is the expectation of a man who holds 10 tickets?
A bag contains four black and five red balls. If three balls from the bag are chosen at random, what is the chance that they are all black?
A bag contains 20 balls marked 1 to 20. One ball is drawn at random. Find the probability that it is marked with a number multiple of 5 or 7.
A bag contains 6 red, 4 white and 8 blue balls. If three balls are drawn at random, find the probability that all the three balls are of the same colour.
|
191 videos|131 docs|110 tests
|
|
191 videos|131 docs|110 tests
|