Quadrilaterals - Olympiad Level MCQ, Class 9 Mathematics - Class 9 MCQ
25 Questions MCQ Test - Quadrilaterals - Olympiad Level MCQ, Class 9 Mathematics
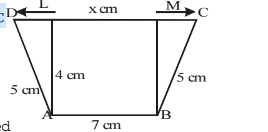
In the given figure, ABCD is a trapezium in which AB = 7 cm, AD = BC = 5 cm, DC = x cm and the distance between AB and DC is 4 cm. Then the values of x is
ABCD is a quadrilateral. If AC and BD bisect each other then ABCD must be
ABCD is a parallelogram. The angle bisectors of ∠A and ∠D meet at O. The measure of ∠AOD is
The diameter of circumcircle of a rectangle is 10 cm and breadth of the rectangle is 6 cm. Its length is
ABCD and MNOP are quadrilaterals as shown in the figure below. Then
If ABCD is a parallelogram, then ∠A – ∠C
One of the diagonals of a rhombus is equal to a side of the rhombus. The angles of the rhombus are
The diagonals of a parallelogram ABCD intersect at O. If ∠BOC = 90° and ∠BDC = 50°, then ∠AOB is
ABCD is a rhombus. ∠If ACB = 40°, then ∠ADB is
In a quadrilateral PQRS, if ∠P = ∠R = 100° and ∠S = 75° then ∠Q =
If the lengths of two diagonals of a rhombus are 12 cm and 16 cm, then the length of each side of the rhombus is
In a quadrilateral, the angles are in the ratio 3 : 4 : 5 : 6. Then the difference between the greatest and the smallest angle is:
In a quadrilateral ABCD, ∠A + ∠C + 180° then ∠B + ∠D =
Which of the following statement(s) is / are false ?
The angles of a quadrilateral are x°, x – 10°, x + 30° and 2x°. Find the greatest angle
In a parallelogram ABCD, if∠A = 80° then ∠B=
In a trapezium ABCD, AB || CD if ∠A = 50° then ∠D =
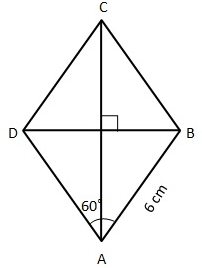
In a rhombus ABCD, ∠A = 60° and AB = 6 cm. Find the diagonal BD
In a square ABCD, its diagonals bisect at O. Then the triangle AOB is
Which of the following properties are not true for a parallelogram ?
In a rhombus ABCD, the diagonals intersect at O. If AB = 10 cm, diagonal BD = 16 cm, then the length of
the diagonal AC is .............
The perimeter of a parallelogram is 180 cm. One side exceeds the another by 10 cm. The adjacent sides of
the parallelogram are .............
ABCD is a parallelogram in which ∠DAO = 40°, ∠BAO = 35° and ∠COD = 65° then ∠ODC = ..........
ABCD is a parallelogram in which ∠DAB = 75° and ∠DBC = 60° then ∠CDB = .............
In the adjoining figure, AP and BP are angle bisectors of ∠A and ∠B which meet at P of the parallelogram ABCD. Then 2∠APB