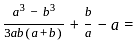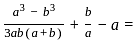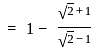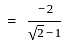RRB NTPC Mathematics Test - 4 - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test RRB NTPC Mock Test Series 2025 - RRB NTPC Mathematics Test - 4
Height of a cone is 12 cm and radius of its base is 3.5 cm. What is the volume of the cone?
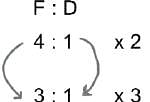
In a pharma company, a scientist is mixing the purified form of Acetone and Toluene to invent some medicine. The cost of the solution obtained after mixing Acetone and Toluene is Rs. 16 per litre. Acetone costs Rs. 14 per litre to the scientist. Due to storage issue, Toluene’s cost is expensive than Acetone to the scientist. The ratio of Toluene to Acetone in the solution is 4 ∶ 1. What is the cost of Toluene per litre (in Rs.) to the scientist?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Alloy A contains metals x and y only in the ratio 5 ∶ 2, while alloy B contains them in the ratio 3 ∶ 4. Alloy c is prepared by mixing alloys A and B in the ratio 4 ∶ 5. the percentage of x in alloy C is:
The total cost of 90 articles is Rs. 5400. If 70 such articles are sold at a total price of Rs. 5040, then there is
The following table shows the income (in Rs.) of five different persons (A, B, C, D, E) over given 4 years.
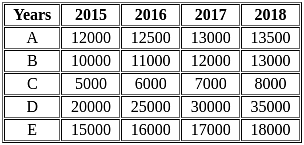
Find the average income of the five persons in year 2015.
Due to engine trouble, an Express train goes at 9/10th of its usual speed and arrives at 2 : 34 pm instead of 2 : 28 pm. At what time did it start?
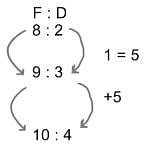
On dividing a number by 42, we get 120 as the quotient and 0 as the remainder. On dividing the same number by 41, what will be the remainder?
If Secθ = 4/3, what is the value of tan2 θ + tan4 θ?
Pipe A can fill a tank in X hours. Pipe B can empty it in 15 hours. If both the pipes are opened together, then the tank will be filled in 7 hours and 30 minutes. Find X.
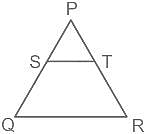
In the given figure ST || QR and ST ∶ QR = 3 ∶ 8. The ratio of the area of ΔPST and trapezium QRTS is
Mr. Ayush borrowed Rs. 3000 at 5% per annum compound interest. The compound interest compounded annually for 2 years is:
Father is four times the age of his daughter. If after 5 years, he would be three times of daughter's age, then further after 5 years, how many times he would be of his daughter's age?
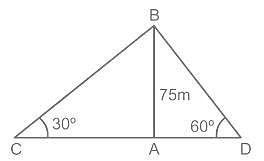
Two men on both side of a tower 75 m high observe the angle of elevation of the top of the tower to be 30° and 60°. What is the distance between two men?
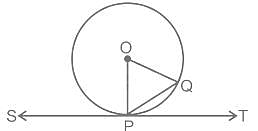
In the figure given below, SPT is a tangent to the circle at P and O is the centre of the circle. If ∠QPT = α, then what is ∠POQ equal to?
Directions: The following pie chart shows the expenditure (in percentage) of five companies P, Q, R, S and T in one year 2020.

What was the total expenditure in (Rs Cr) of the company Q, R & T together?
The centroid of an equilateral triangle ABC is G and AB = 12 cm. The length of AG (in cm) is :
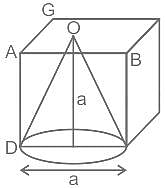
Find the volume (in cm3) of the largest right circular cone that can be cut out of a cube where the edge is 9 cm.
A solid sphere has a surface area of 616 cm2. This sphere is now cut into two hemispheres. What is the total surface area of one of the hemispheres?
In ΔABC, ∠C = 90°, BC = AC = 3√2, then AB = __________.


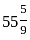
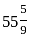
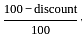 × marked price
× marked price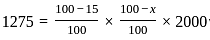
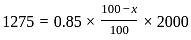
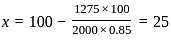
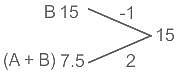
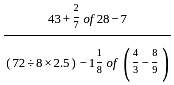 is
is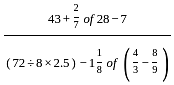
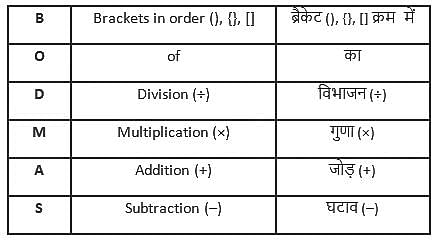
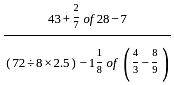
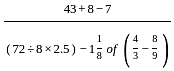
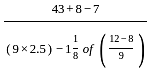
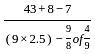
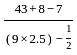
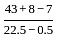
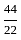 = 2
= 2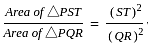
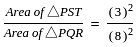
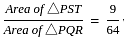
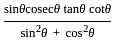 is
is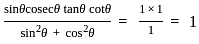
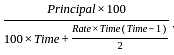
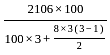
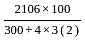
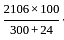
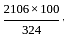
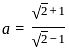 and
and 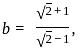 then the value of
then the value of