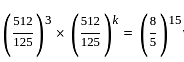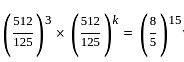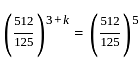RRB NTPC Mathematics Test - 5 - RRB NTPC/ASM/CA/TA MCQ
30 Questions MCQ Test RRB NTPC Mock Test Series 2025 - RRB NTPC Mathematics Test - 5
Sumit earned Rs. 10,692 as simple interest on Rs. 29,700 at a certain rate of interest for 3 years. His friend Anil invested Rs. 12,500 for 2 years at the same rate of interest but on compound interest compounded annually. How much did Anil earn as interest?
Which among the following is a rational number equivalent to 3/5
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The marked price of an item is Rs. 15,800. If a shopkeeper earns a profit of 18% after allowing a discount of 20%, then the cost price (in Rs.) of the item (nearest to Rs. 1) is:
There is a circular path around a sports field. Rahul takes 15 minutes to drive one round of the field, while Anil takes 18 minutes for the same. Suppose they both start from the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
A starts a business with ₹75,000 and B joins the business 5 months later with an investment of ₹80,000. After 1 year, they earn a profit of ₹4,08,800. Find the share of A and B (in ₹).
A shopkeeper decides to sell a certain item at a certain price. He tags the price on the item by increasing the decided price by 45%. While selling the item, he offers 40% discount. Find how much more or less he gets on the decided price.
Length of the one diagonal of a rhombus is 30 cm. If the area of the rhombus is 300 cm2, then what will be length of the other diagonal?
In a competitive examination held in the year 2000, a total of 6,00,000 (6.0 lakh) students appeared and 40% passed the examination. Forty percent (40%) of the total students. were females and the rest were males. The pass percentage among the males was 50%. Find the pass percentage among the females.
In an election, a candidate who gets 70% of the votes is elected by a majority of 500 votes. What is the total number of votes?
After a certain time period, a sum of Rs. 24,000 invested in a bank will amount to Rs. 26,460 when the compound rate of interest is 5% p.a., being compounded annually. In how many months will it amount to Rs. 26,460?
The following table gives the sales of LCDs manufactured by a company over they years since its inception.
Number of Different Sizes of LCDs Sold by a Company Over the Years (Numbers in Thousands)
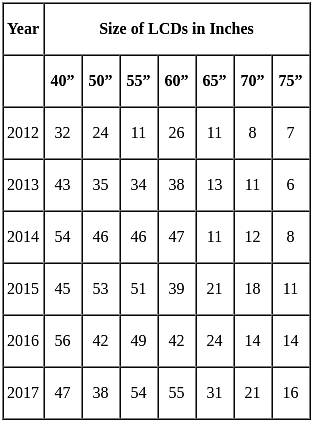
The total sales of all the six years are the minimum for which size LCD TV?
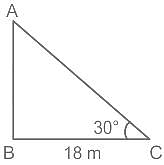
A tree breaks due to storm and the broken part bends, so that the top of the tree touches the ground making an angle of 30° with the ground. The distance between the foot of the tree to the point where the top touches the ground is 18 m. Find the height of the tree (in metres)
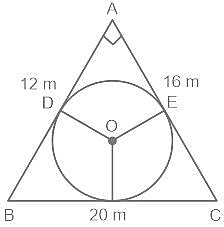
Rajan design a map of a house, whose front is in a shape of a right angles triangle and a circular door is fitted in it. The lenghts of the two sides containing the right angle are 12 and 16m. Find the radius of the circle.
If a + b = 20 and ab = 75 then find the value of a3 + b3
Two pipes P1 and P2 can fill an empty tank in 6 hours and 8 hours respectively. Pipe P3 can empty that completely filled tank in 16 hours. First both the pipes P1 and P2 are opened and after 3 hours pipe P3 is also opened. In what time will the tank be completely filled?
Pratik lends Rs 8000 to his friend at 10% per annum of compound interest, in how many years it will become Rs 9261 if compounded semiannually.
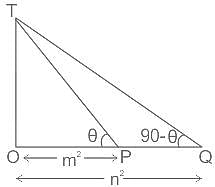
The angles of elevation of the top of a tower from two points P and Q at distances m2 and n2 respectively, from the base and in the same straight line with it are complementary. The height of the tower is
In a meeting of 45 people, there are 40 people who know one another and the remaining know no one. People who know each other only hug, whereas those who do not know each other only shake hands. How many handshakes occur in this meeting?
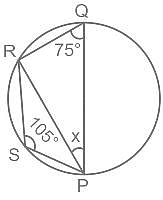
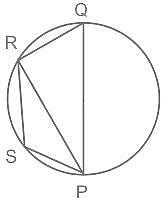
In the given figure, ∠PSR = 105° and PQ is the diameter of the circle. What is the value (in degrees) of ∠QPR?
What is the probability that the month of December has 5 Sundays ?
If marked price of a articles is 25% more than cost price and discount given on the article is 10%. Find profit percentage on the article
Ram Lal is making Lassi in his shop. While making a glass of lassi, he uses 5/6 of curd and the rest is milk. Find the quantity of mixture in ratio taken away and substituted by equal quantity of milk so as to have half curd and half milk.
Ramesh invested Rs. 100000 at compound interest and same amount at simple interest in two different banks both giving 5% rate of interest per annum. What is the difference between the interest earned in two years?
A ladder is resting against a vertical wall and its bottom is 2.5 m away from the wall. If it slips 0.8 m down the wall, then its bottom will move away from the wall by 1.4 m. What is the length of the ladder?


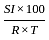

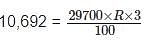

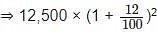
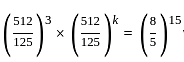 , then k is:
, then k is: