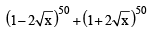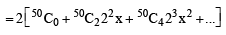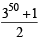Test: 35 Year JEE Previous Year Questions: Mathematical Induction and Binomial Theorem - JEE MCQ
27 Questions MCQ Test 35 Years Chapter wise Previous Year Solved Papers for JEE - Test: 35 Year JEE Previous Year Questions: Mathematical Induction and Binomial Theorem
The coefficients of xp and xq in the expansion of (1+ x)p+q are[2002]
If the sum of the coefficients in the expansion of ( a + b)n is 4096, then the greatest coeficient in the expansion is [2002]
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The positive integer just greater than (1 + 0.0001)10000 is [2002]
r and n are positive integers r > 1, n > 2 and coefficient of (r+2)th term and 3rth term in the expansion of (1 + x)2n are equal, then n equals [2002]
If 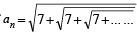 haing n radical signs then by methods of mathematical induction which is true [2002]
haing n radical signs then by methods of mathematical induction which is true [2002]
If x is positive, the first negative term in the expansion of (1 + x)27/5 is [2003]
The number of integral terms in the expansion of 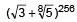 is [2003]
is [2003]
Let S(K) = 1 + 3 + 5... + (2K - 1) =3+K 2 . Then which of the following is true [2004]
The coefficient of the middle term in the binomial expansion in powers of x of (1 + αx)4 and of (1 - αx)6 is the same if a equals [2004]
The coefficient of xn in expansion of (1 + x) (1 – x)n is
The value of 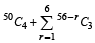 [2005]
[2005]
IF  then which one of the following holds for all n ≥ 1, by the principle of mathematical induction [2005]
then which one of the following holds for all n ≥ 1, by the principle of mathematical induction [2005]
If the coefficient of x 7 in 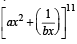 equals the coefficient of x -7 in
equals the coefficient of x -7 in  , then a and b satisfy the relation [2005]
, then a and b satisfy the relation [2005]
If x is so small that x3 and higher powers of x may be neglected, then 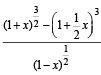 may be approximated as [2005]
may be approximated as [2005]
If the expansion in powers of x of the function 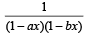 is a0 + a1 x + a2 x2+ a3x3 ...... then an is [2006]
is a0 + a1 x + a2 x2+ a3x3 ...... then an is [2006]
For natural numbers m, n if (1 – y)m (1 + y)n = 1 + a1y + a2y2 + ....... and a1 = a2 = 10, then (m, n) is
In the binomial expansion of (a – b)n, n ≥ 5, the sum of 5th and 6th terms is zero, then a/b equals
The sum of the series 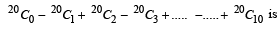 is [2007]
is [2007]
Statement -1 : 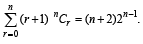 [2008]
[2008]
Statement-2 : 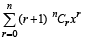
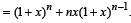
The remainder left out when 82n – (62)2n +1 is divided by 9 is :[2009]
Let 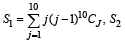
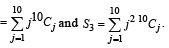
Statement-1 : S3 = 55 × 29
Statement-2: S1 = 90 × 28 and S2 = 10 × 28 . [2010]
The coefficient of x7 in the expansion of (1– x – x2 + x3 )6 is [2011]
If n is a positive integer , then 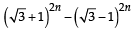 is
is
The term independent of x in expansion of 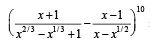 is [JEE M 2013]
is [JEE M 2013]
If the coefficents of x3 and x4 in the expansion of (1 + ax + bx2 ) (1-2 x )18 in powers of x are both zero, then (a, b) is equal to: [JEE M 2014]
The sum of coefficients of integral power of x in the binomial expansion 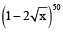 is: [JEE M 2015]
is: [JEE M 2015]
If the number of terms in th e expan sion of 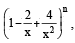 x ≠ 0, is 28, then the sum of the coefficients of all the terms in this expansion, is : [JEE M 2016]
x ≠ 0, is 28, then the sum of the coefficients of all the terms in this expansion, is : [JEE M 2016]
|
347 docs|185 tests
|
|
347 docs|185 tests
|


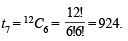
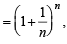 n = 10000
n = 10000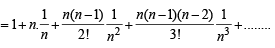
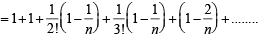

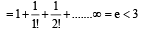
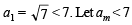
 = 7 + am < 7 + 7 < 14.
= 7 + am < 7 + 7 < 14.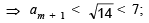 So by the prin ciple of mathematical induction an < 7 ∀ n.
So by the prin ciple of mathematical induction an < 7 ∀ n.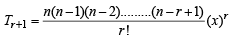
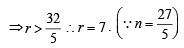
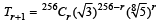
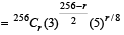
 both are +ve
both are +ve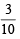
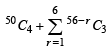

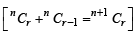 ⇒ (50 C4 +50C3)
⇒ (50 C4 +50C3)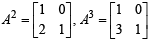 and we can prove by
and we can prove by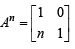

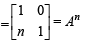
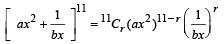
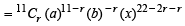
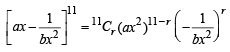
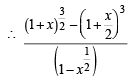
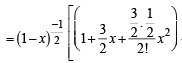
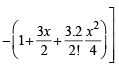
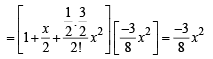
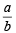
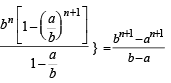
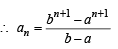
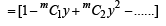

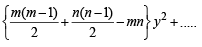
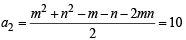
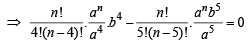
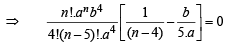
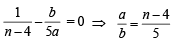
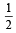 20C10
20C10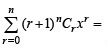
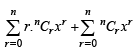
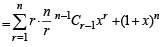
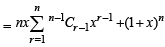

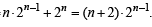
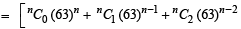
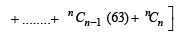
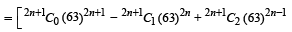
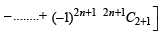
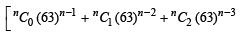 +........]+ 1
+........]+ 1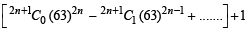
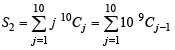
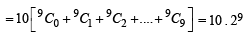

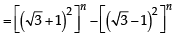
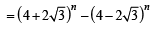
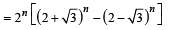
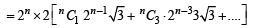
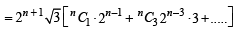
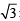 x Some integer ∴ irrational number
x Some integer ∴ irrational number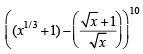
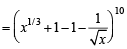
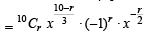
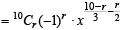
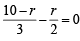
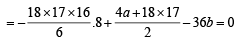
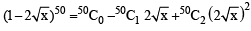 ...(1)
...(1)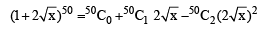
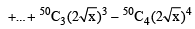 ...(2)
...(2)