Test: Applications Of Mathematical Induction - Commerce MCQ
15 Questions MCQ Test Online MCQ Tests for Commerce - Test: Applications Of Mathematical Induction
For each n ∈ N, 72n + 16n – 1 is divisible by :
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
2.42n + 1 + 33n + 1 for all n is divisible by λ for all n ∈ N” is true, then the value of λ is ____
The sum of cubes of three consecutive natural numbers is divisible by:
If 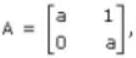 then for some n ∈ N, An is equal to :
then for some n ∈ N, An is equal to :
The smallest positive integer n, for which
To prove a formula by principle of mathematical induction, we verify the statement
The greatest natural number, which divides (n + 1) (n +2) (n + 3)(n + 4) is
If P(k) is the statement 23k – 1 is divisible by 7, then P(k + 1) is
For each n ∈ N, n(n + 1) (2n + 1) is divisible by:
Let P(n) is the statement the product of two consecutive natural numbers is even. Then which of the following is true?
For positive integers n, (1 + x)n > 1 + nx ; (x > – 1) when
Let P(n) b e a statement 2n<n! where n is a natural number, then P(n) is true for
The principle of mathematical induction is for the set of:
|
705 tests
|

















