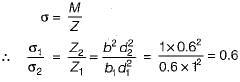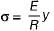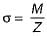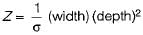Test: Bending Stresses in Beams - Mechanical Engineering MCQ
10 Questions MCQ Test - Test: Bending Stresses in Beams
A 0.2 mm thick tape goes over a frictionless pulley of 25 mm diameter. If E of the material is 100 GPa, then the maximum stress induced in the tape is


A cantilever beam of rectangular cross-section is 1 m deep and 0.6 m thick. If the beam were to be 0.6 m deep and 1 m thick then the beam would
The assumption “the plane section before bending remains plane after bending” made in the theory of bending implies:
For a beam of uniform strength, if its depth is kept constant, then its width will vary in proportion to
When a rectangular beam is loaded longitudinal, shear develops on
A rod of length L and diameter D is subjected to a tensile load P. Which of the following is sufficient to calculate the resulting change in diameter?
Beams of uniform strength so vary in section that the


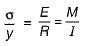 (Bending formula)
(Bending formula)