CAT Exam > CAT Tests > Daily Test for CAT Preparation > Test: Binary Logic (April 24) - CAT MCQ
Test: Binary Logic (April 24) - CAT MCQ
Test Description
10 Questions MCQ Test Daily Test for CAT Preparation - Test: Binary Logic (April 24)
Test: Binary Logic (April 24) for CAT 2024 is part of Daily Test for CAT Preparation preparation. The Test: Binary Logic (April 24) questions and answers have been
prepared according to the CAT exam syllabus.The Test: Binary Logic (April 24) MCQs are made for CAT 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Binary Logic (April 24) below.
Solutions of Test: Binary Logic (April 24) questions in English are available as part of our Daily Test for CAT Preparation for CAT & Test: Binary Logic (April 24) solutions in
Hindi for Daily Test for CAT Preparation course. Download more important topics, notes, lectures and mock
test series for CAT Exam by signing up for free. Attempt Test: Binary Logic (April 24) | 10 questions in 20 minutes | Mock test for CAT preparation | Free important questions MCQ to study Daily Test for CAT Preparation for CAT Exam | Download free PDF with solutions
Test: Binary Logic (April 24) - Question 1
Three persons Bryan, Edward and Avril, each of whom is of a different community, are standing together. When asked about their community, Bryan replied, "I am a Gitty. Avril is Amora.". Then Edward belongs to which community?
Detailed Solution for Test: Binary Logic (April 24) - Question 1
Test: Binary Logic (April 24) - Question 2
Each of three different persons Mary, Helen and Patricia belong to a different community. In the conversation, Patricia said, "I am a Pixie. Mary is not a Gitty.'' Who among the three persons is an Amora?
Detailed Solution for Test: Binary Logic (April 24) - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Binary Logic (April 24) - Question 3
If Bruce is not a Pixie, then who among the three persons is the Gitty?
Detailed Solution for Test: Binary Logic (April 24) - Question 3
Detailed Solution for Test: Binary Logic (April 24) - Question 4
Detailed Solution for Test: Binary Logic (April 24) - Question 5
Test: Binary Logic (April 24) - Question 6
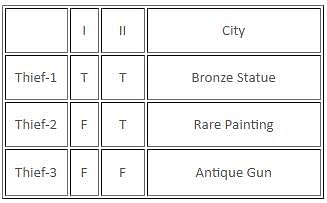
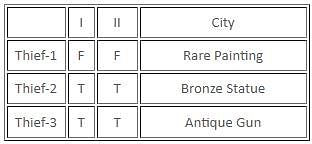
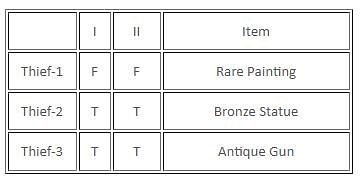
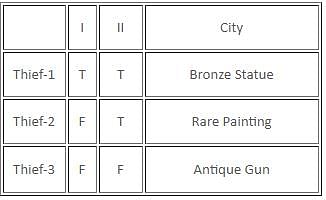
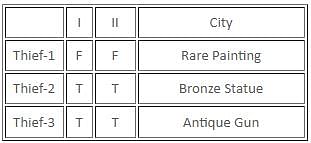
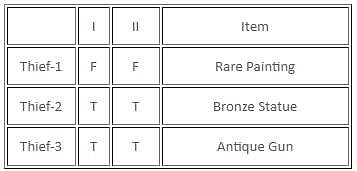
If there are exactly two thieves who always tell the truth and the third thief either always lies or alternates between the truth and a lie, then which of the following statements must be false?
Detailed Solution for Test: Binary Logic (April 24) - Question 6
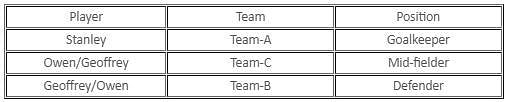
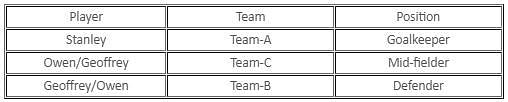
Detailed Solution for Test: Binary Logic (April 24) - Question 7
Detailed Solution for Test: Binary Logic (April 24) - Question 8
Detailed Solution for Test: Binary Logic (April 24) - Question 9
Detailed Solution for Test: Binary Logic (April 24) - Question 10
|
152 docs|327 tests
|
Information about Test: Binary Logic (April 24) Page
In this test you can find the Exam questions for Test: Binary Logic (April 24) solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Binary Logic (April 24), EduRev gives you an ample number of Online tests for practice