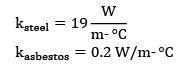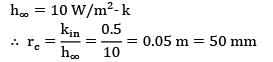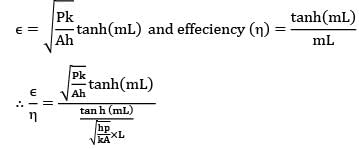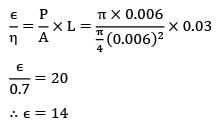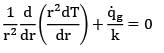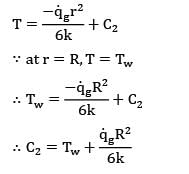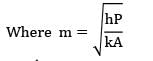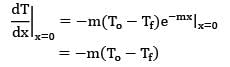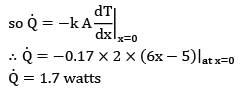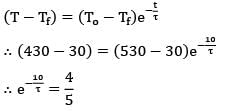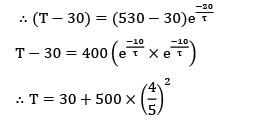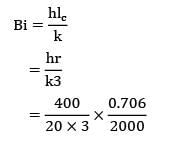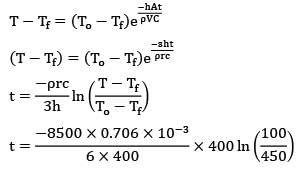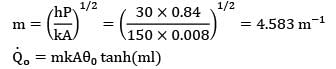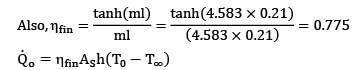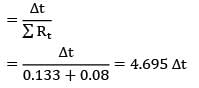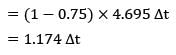Test: Conduction Level - 2 - Mechanical Engineering MCQ
20 Questions MCQ Test - Test: Conduction Level - 2
The temperature distribution, at a certain instant of time in a concrete slab during curing is given by T = 3x2 + 3x + 16, where x is in cm and T is in K. The rate of change of temperature with time is given by (assume thermal diffusivity of concrete to be 0.0003 cm2/s).
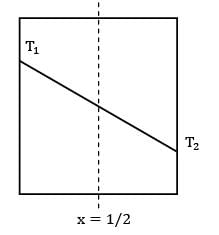
A large concrete slab 1 m thick has one dimensional instantaneous temperature distribution
T = 4 - 10x + 20x2 + 10x3
Where T is temperature in °C and x is distance in m from one face towards the other face of the wall. If the slab material has thermal diffusivity of 2 X 10-3m2/hr, what is the rate of change of temperature at the other face of the wall for the same instant?
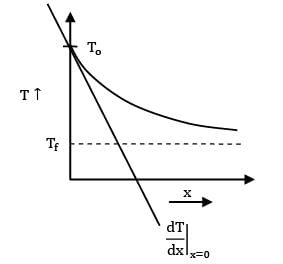
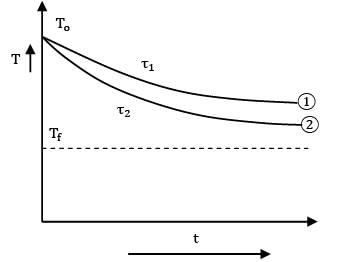
Consider two hot lumps with the same initial temperature To. Both the lumps are dropped in a cold fluid at a constant temperature Tf. If ?1 & ?2 represent time constants of the two lumps, then based on the cooling curve which of the following options is correct.

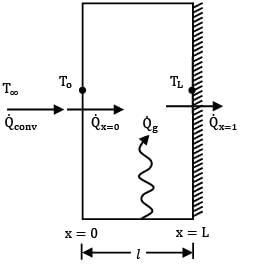
Consider a large plane wall of thickness L, thermal conductivity k and surface area A. The left surface of the wall is exposed to the ambient air at temperature T∞ with a heat transfer coefficient of h while the right surface is insulated. The variation of temperature in the wall for steady state one-dimensional heat conduction with no heat generation is
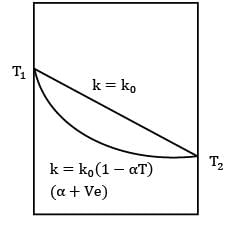
If thermal conductivity of a material of wall varies as k0 (1 - ∝T), the temperature at the center of the wall will be (∝ is + ve)
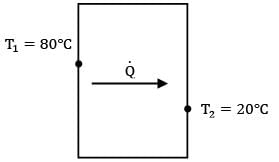
Thermal conductivity of a material varies linearly with temperature such that k = 20 W/m-°C at 100°C&k = 10 W/m-°C at 40°C. A plane slab 10 cm thick of same material has it’s left and right surfaces maintained a temperatures 20°C & 80°C. What is the rate of heat conduction through the slab in W/m2 ?
A hot fluid is being conveyed through a long pipe of 4 cm outer diameter and covered with 2 cm thick insulation. It is proposed to reduce the conduction heat loss to the surroundings to one-third of the present rate by further covering with same insulation. Calculate the additional thickness of insulation.
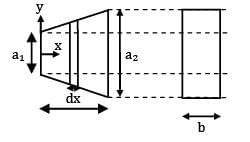
For the body shown in the figure, find out the thermal resistance against heat conduction along the x-axis. Consider the body to be at steady state with no internal heat generation in the material. The material is homogenous
Heat is generated in a 3-cm-diameter spherical radio-active material uniformly at a rate of 15 W/cm3. Heat is dissipated to the surrounding medium at 25°C with a heat transfer coefficient of 120 W/m2-K. The surface temperature of the material in steady operation is
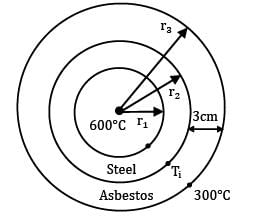
A thick walled tube of stainless steel [18% Cr, 8% Ni,k = 19 W/m ͘· °C] with 2-cm inner diameter (ID) and 4-cm outer diameter (OD) is covered with a 3-cm layer of asbestos insulation [k = 0.2 W/m ͘· °C]. If the inside wall temperature of the pipe is maintained at 600°C calculate the tube-insulation interface temperature. Assume the outermost surface temperature to be 300°C
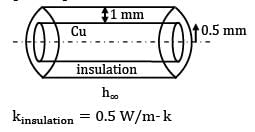
A copper wire of radius 0.5 mm is insulated with a sheathing of thickness 1 mm having a thermal conductivity of 0.5 W/m-K. The outside surface convective heat transfer coefficient is 10 W/m2-K. If the thickness of insulation sheathing is raised by 10 mm, then the electrical current-carrying capacity of the wire will
A cylindrical pin fin of diameter 0.6 cm and length of 3 cm with negligible heat loss from the tip has an efficiency of 0.7. The effectiveness of this fin is
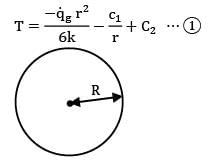
The maximum temperature inside a solid sphere maintained at steady state with one dimensional temperature profile having internal heat generation rate![]() and surface temperature is Tw is
and surface temperature is Tw is
Two very long fins of same length L, perimeter P and area of cross-section A are attached on a surface with temperature To . The surface is exposed to a fluid with temperature Tf & coefficient of convection coefficient h. One fin is made of copper and the other of aluminium. Considering the fins to be at steady state with one dimensional heat transfer which one of the following options represents the correct temperature profile.
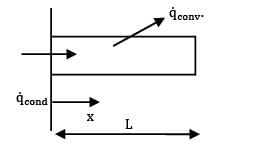
The temperature distribution in a fin (thermal conductivity 0.17 W/cm-°C) with uniform cross-sectional area of 2 cm2 and length of 1 cm exposed to ambient of 40°C (with a surface heat transfer coefficient of 0.0025 W/cm2-°C) is given by (T - T∞ ) = 3x2 - 5x + 6, where T is in °C and x is in cm. If the base temperature is 100°C , then the heat dissipated by the fin surface will be
A small solid copper ball of mass 500 grams, when quenched in a water bath at 30°C cools from 530°C to 430°C in 10 seconds. What will be the temperature of the ball after the next 10 seconds?
A spherical thermocouple junction of diameter 0.706 mm is to be used for the measurement of temperature of a gas stream. The convective heat transfer co-efficient on the bead surface is 400 W/m2K. Thermo-physical properties of thermo couple material are k = 20 W/m-K,C = 400 J/kg- K and
? = 8500 kg/ m3. If the thermocouple initially at 20°C is placed in a hot stream of 500°C, the time taken by the bead to reach 400°C, is
A lump body cools from 90°C to 80°C in 5 minutes. Under the same external conditions, to cool from 80°C to 70°C the body will take
Determine the heat transfer rate from the rectangular fin of length 20 cm, width 40 cm and thickness 2 cm. The tip of the fin is not insulated and the fin has a thermal conductivity of 150 W/m-K. The base temperature is 100°C and the fluid is at 20°C.
The heat transfer coefficient between the fin and the fluid is 30 W/m2-K.
An exterior wall of a house may be approximated by a 10 cm layer of common brick (k = 0.75 W/m-°C) followed by a 4 cm layer of gypsum plaster (k = 0.5w/m-°C). What thickness of loosely packed rock wool insulation (k = 0.065 W/m-°C) should be added to reduce the heat loss or gain through the wall by 75% ?


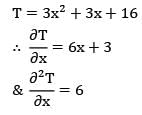
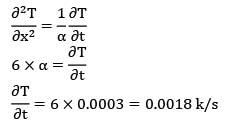
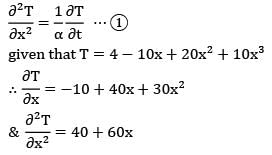
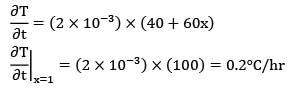

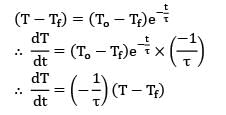
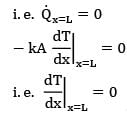
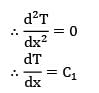
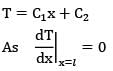
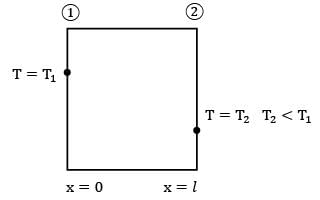
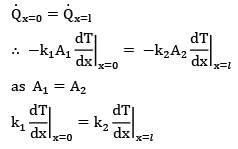
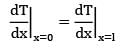
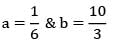
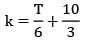
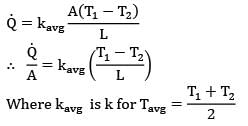
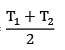
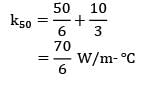
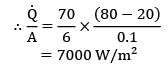
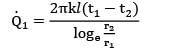
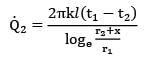
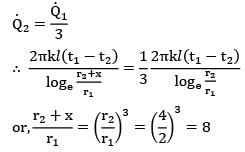
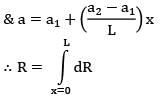
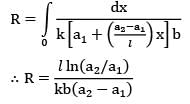
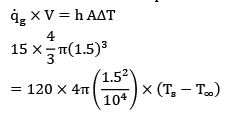
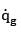 is given in W/cm3 but in R.H.S, radius is put in m because h is given in W\m2-k.
is given in W/cm3 but in R.H.S, radius is put in m because h is given in W\m2-k.