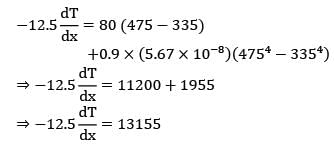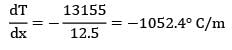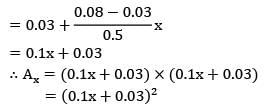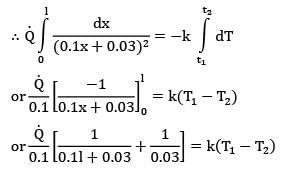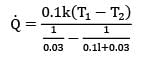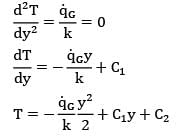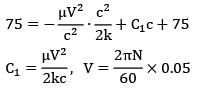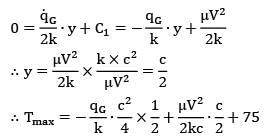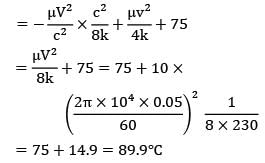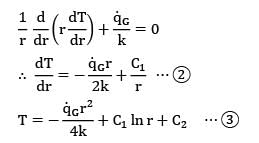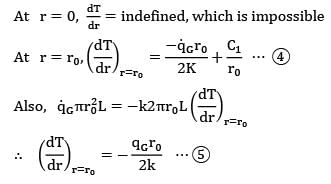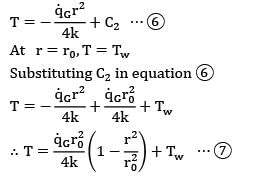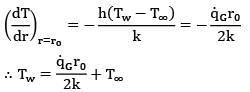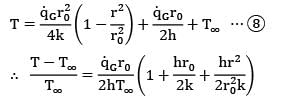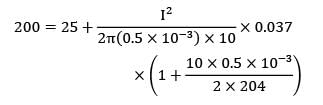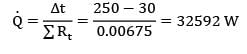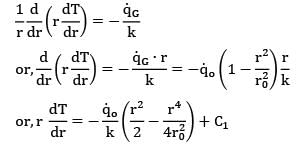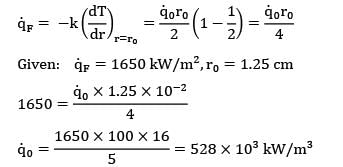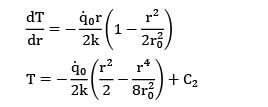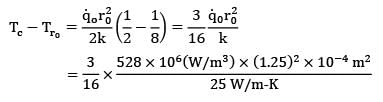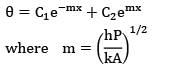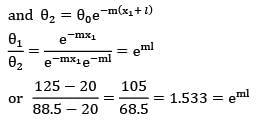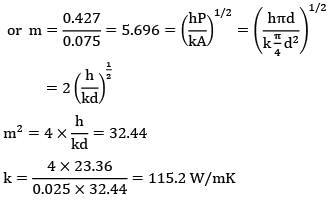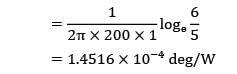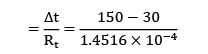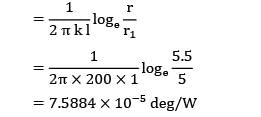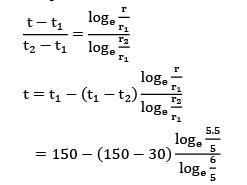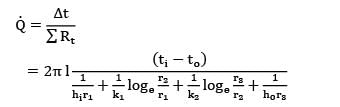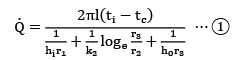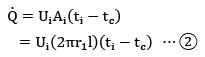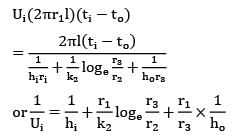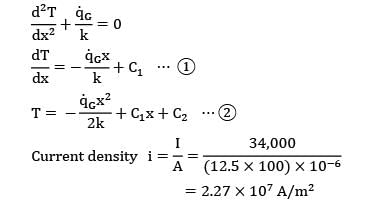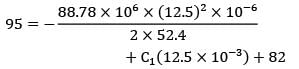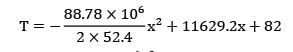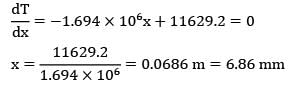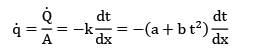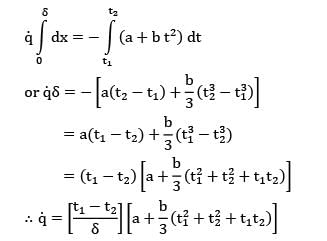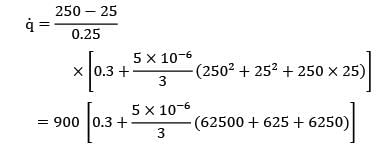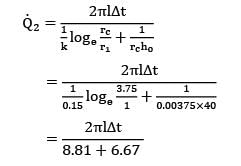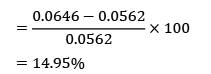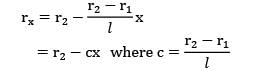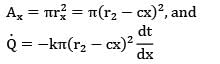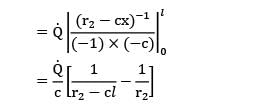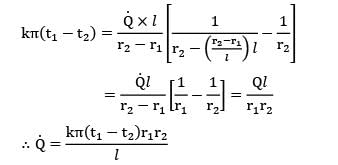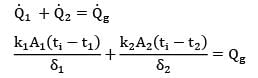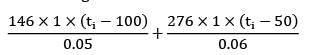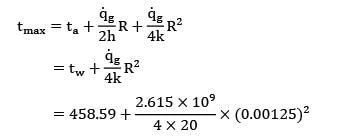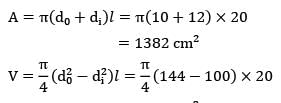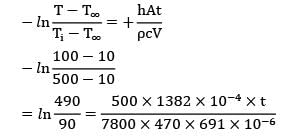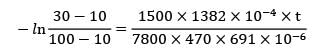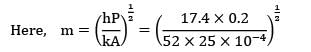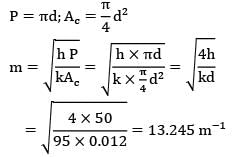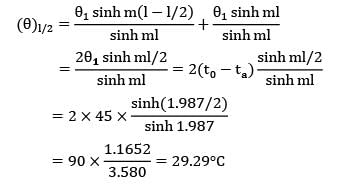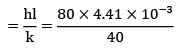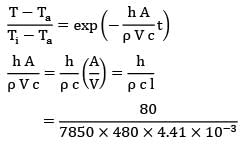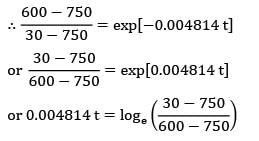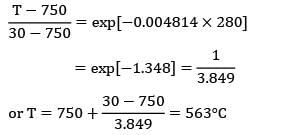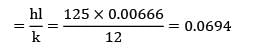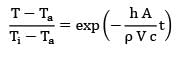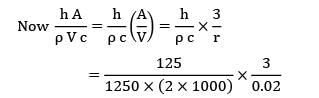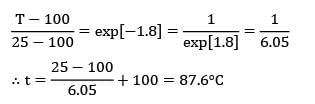Open App

Mechanical Engineering Exam > Mechanical Engineering Tests > Heat Transfer > Test: Conduction Level - 3 - Mechanical Engineering MCQ

Test: Conduction Level - 3 - Mechanical Engineering MCQ

Test Description

20 Questions MCQ Test Heat Transfer - Test: Conduction Level - 3

Test: Conduction Level - 3 for Mechanical Engineering 2024 is part of Heat Transfer preparation. The Test: Conduction Level - 3 questions and answers have been prepared according to the Mechanical Engineering exam syllabus.The Test: Conduction Level - 3 MCQs are made for Mechanical Engineering 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Conduction Level - 3 below.

Solutions of Test: Conduction Level - 3 questions in English are available as part of our Heat Transfer for Mechanical Engineering & Test: Conduction Level - 3 solutions in Hindi for Heat Transfer course. Download more important topics, notes, lectures and mock test series for Mechanical Engineering Exam by signing up for free. Attempt Test: Conduction Level - 3 | 20 questions in 60 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study Heat Transfer for Mechanical Engineering Exam | Download free PDF with solutions

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 1

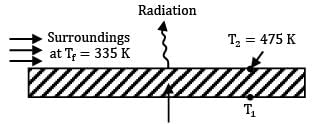
A surface at 475 K convects and radiates heat to the surroundings at 335 K. If the surface conducts this heat through a solid plate of thermal conductivity 12.5 W/m-°C, determine the temperature gradient at the surface in the solid. Take convective coefficient and emissivity as 80 W/m²-°C and 0.9 respectively

Detailed Solution for Test: Conduction Level - 3 - Question 1

Under steady state conditions, the heat rate of conduction through the plate equals the sum of rate of convection and radiation through the surface. That is

Heat conducted through the plate

= convection heat losses

+ radiation heat losses

Taking unit area and substituting the relevant data, we have

∴ Temperature gradient through the plate,

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 2

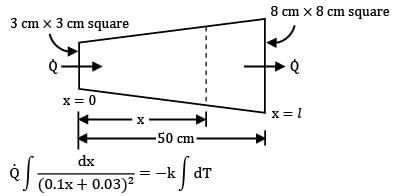
Heat is conducted through a uniformly tapered rod of square cross-section and length 50 cm. At the left end, the side of face is 3 cm and the temperature is 600°C. At the right end, the corresponding values are 8 cm and 150°C. Determine the rate of heat conduction. It may be presumed that thermal conductivity of the material of rod is 60 W/mK and heat is conducted only along the length of rod.

Detailed Solution for Test: Conduction Level - 3 - Question 2

For one-dimensional heat conduction in the x-direction, we have

Where A_x is the cross-sectional area at a distance x from the smaller end of the rod.

Side of face at distance x meter from the small end

From the fourier heat conduction equation

Separating the variables and upon integration

The boundary conditions are:

At x = 0, T = T₁ = 600°C

At x = ? = 0.5 m, T = T₂ = 150°C

∴ Heat flow,

1 Crore+ students have signed up on EduRev. Have you? Download the App

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 3

An oil film acts as a lubricant (? = 10 N-s/m², k = 230 W/m-K,? = 1200 kg/m³) between two coaxial cylindrical surfaces (outer diameter and inner diameter = 99.5 mm). The outer cylinder rotates at . Calculate the maximum temperature in the oil film if both wall temperatures are maintained at 75°C. The rate of heat generation per unit volume due to viscous dissipation may be assumed to be 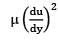. As the oil layer is very thin ignore any convection in the layer.

Detailed Solution for Test: Conduction Level - 3 - Question 3

Since the clearance between two cylinders is very small, the velocity variation in the oil may be assumed to be linear. At any point in the oil, the heat conduction equation can be given as

Where

At y = 0, T = 75°C, ∴ C₂ = 75°C

At y = C, T = 75°C,

For maximum temperature =

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 4

A 1 mm dia aluminium (k = 204 W/m-K) wire can carry a current till wire temperature does not exceed T_max = 200°C when suspended in air at 25°C where h = 10 W/m²K. For the wire, the specific resistance is 0.037 ohm/m. The maximum current the wire can carry is __________A.

Detailed Solution for Test: Conduction Level - 3 - Question 4

Heat conducted to the outside surface of the wire = Heat convected to the air,

where T_w is the outside surface temperature of the wire. At the centre, T is maximum and

From the heat conduction equation,

From equation and , C₁= 0

Equation reduces to

From Equation ,

Substituting T_w in Equation , we get the temperature distribution,

Putting r = 0, T = T_max

I_max = 12.19 amperes

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 5

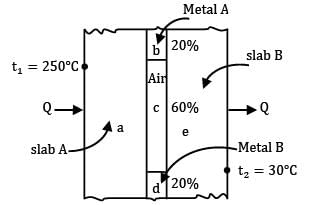
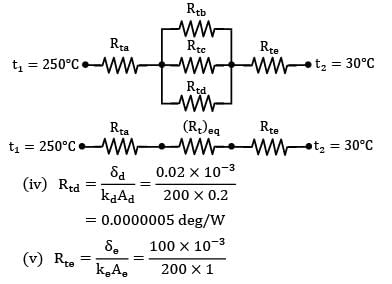
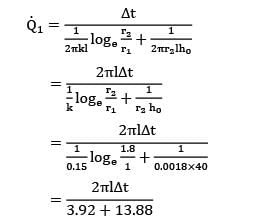
Two slabs, each 100 mm thick and made of materials with thermal conductivities of 16 W/m-deg and 1600 W/m-°C, are placed in contact which is not perfect. Due to roughness of surfaces, only 40% of the area is in contact and air fills 0.02 mm thick gaps in the remaining area. If the extreme surfaces of the arrangement are at temperatures of 250°C and 30°C, determine the heat flow rate through the composite system.

Take thermal conductivity of air as 0.032 W/m-°C and assume that half of the contact (of the contact area) is due to either metal.

Detailed Solution for Test: Conduction Level - 3 - Question 5

Refer figure for the composite system and it’s equivalent thermal resistance The various thermal resistances to flow of heat are

= 0.00000625 deg/W

= 0.0005 deg/W

The resistances R_tb, R_tc and R_td are in a parallel connection and their equivalent resistance (R_t)_eq is

This equivalent resistance is now in series with resistance R_ta and R_te, the total thermal resistance for the entire circuit then becomes

= 0.00675 deg/W

Hence, heat transfer rate through the system is

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 6

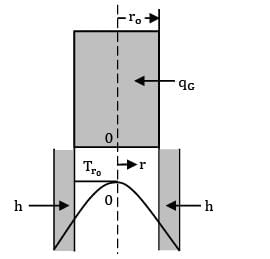
In a cylindrical fuel rod of a nuclear reactor, heat is generated internally according to the equation where is the local rate of heat generation per unit volume at radius r,r₀ is the outside radius, and is the rate of heat generation per unit volume at the centre line. Calculate the temperature drop from the centre line to the surface for a 2.5 cm outer diameter rod having k = 20 W/m-K, if the rate of heat removal from the surface is 1650 kW/m².

Detailed Solution for Test: Conduction Level - 3 - Question 6

In cylindrical coordinates, the radial variation of temperature at steady state when there is internal heat generation is given by figure

Heat transferred from the rod

This is the volumetric heat generation at the centre line of the rod. Now,

At , r = 0, T = T_c, the centre line temperature

C₂ = T_c

At, r = r₀, the temperature drop,

= 618.7°C

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 7

One end of a long rod is inserted into a furnace while the other projects into ambient air. Under steady state the temperature of the rod is measured at two points 75 mm apart and found to be 125°C and 88.5°C.respectively, while the ambient temperature is 20°C. If the rod is 25 mm in diameter and h is 23.36 W/m²-K, find the thermal conductivity of the rod material.

Detailed Solution for Test: Conduction Level - 3 - Question 7

The temperature distribution is given by

At x = 0, ? = ?₀, and at x → ∞,? = 0

∴ C₂ = 0

? = C₁e^-mx

Let ? be the distance between the two points where the temperatures are measured. Then,

?₁ = ?₀e^-mx1

ml = 0.427

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 8

Hot combustion gases at 150°C flow through a hollow cylindrical pipe of 10 cm inner diameter and 12 cm outer diameter. The pipe is located in a space at 30°C and the thermal conductivity of the pipe material is 200 W/m-K. Neglecting surface heat transfer coefficients, calculate the temperature at a point halfway between the inner and outer surface.

Detailed Solution for Test: Conduction Level - 3 - Question 8

In terms of geometrical parameters, thermal resistance of a cylindrical pipe is

Heat loss

= 826674 W

Radius at halfway through the pipe wall,

Thermal resistance of cylindrical pipe up to its mid-plane

Since heat flow through each section is same

∴ Temperature at the midplane,

T = 150 - 826674 X 7.5884 X 10^-5

= 87.27°C

Alternatively from the expression for temperature distribution

= 87.18°C

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 9

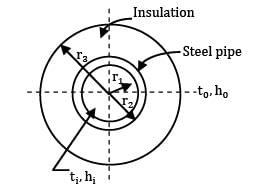
A steel pipe of 20 mm inner diameter and 2 mm thickness is covered with 20 mm thick fiberglass insulation(k = 0.05 W/m-°C). If the inside and outside convective coefficients are 10 W/m²-°C and 5W/m²-°C , calculate the overall heat transfer coefficient based on inside diameter of the pipe.

Detailed Solution for Test: Conduction Level - 3 - Question 9

r₁ = 10 mm ; r₂ = 10 + 2 = 12 mm and r₃

= 12 + 20 = 32 mm

The thermal resistance to flow of heat are offered by

The heat transfer through the insulated pipe is than given by

The thermal conductivity of steel pipe is not given, and generally it is much higher than that of insulation. Accordingly thermal resistance due to pipe material can be neglected

That gives:

if U_i is the overall heat transfer coefficient based on inside surface area of the steel pipe, then heat flow rate can also be written as

comparing identities and , we note that

Upon substitution of given data,

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 10

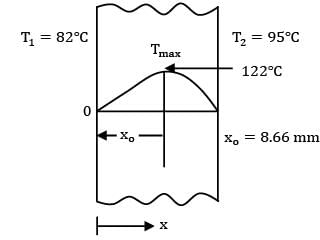
An electric current of 34,000 A flows along a flat steel plate 12.5 mm thick and 100 mm wide. The temperature of one surface of the plate is 82°C and that of the other is 95°C and the value of the maximum temperature.

Detailed Solution for Test: Conduction Level - 3 - Question 10

The temperature distribution in the plate (Figure) is obtained from

= 88.78 X 10⁶ W/m³

From equation , at x = 0, T = 82°C

C₂ = 82°C

At x = 12.5 X 10^-3 m,T = 95°C

From equation ,

= -50.37 + C₁(12.5 X 10^-3)

C₁ = 11629.2 (K/m)

= -0.847 X 10⁶x² + 11629.2x + 82

It is the temperature distribution across the plate. For the maximum temperature,

T_max= -0.847 X10⁶ X (0.00686)² + 11629.2

X 0.00686 + 82

= -39.86 + 79.78 + 82 = 121.92°C

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 11

For a furnace wall of thickness the thermal conductivity varies with temperature according to the relation

k = (a+bt²)W/m-°C where t is in °C Proceed to calculate the rate of heat transfer through the wall if ? = 0.25 m, t₁ = 250°C, t₂ = 25°C, a = 0.3 & b = 5 X 10^-6 in W/m²

Detailed Solution for Test: Conduction Level - 3 - Question 11

Invoking Fourier’s law of heat conduction

Separating the variables and integrating within the prescribed boundary conditions,

we get

which is the required expression Substituting the given data, the rate of heat transfer through the wall works out as

= 374.06 W/m²

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 12

A 2 mm diameter wire with 0.8 mm thick layer of insulation (k = 0.15 W/m-°C) is used in a certain electric heating application. The insulation surface is exposed to the atmosphere with convective heat transfer coefficient 40 W/m²-°C. What percentage change in heat transfer rate would occur if critical thickness of insulation is used? It may be assumed that temperature difference between surface of the wire and surrounding air remains unchanged

Detailed Solution for Test: Conduction Level - 3 - Question 12

Case I: r₁ = 1 mm; r₂ = 1 + 0.8 = 1.8 mm

Heat loss from the wire,

= 0.0562 X (2????)

Case II: The critical radius of insulation for the pipes,

= 0.00375 m = 3.75 mm

Heat loss from the wire when provided with critical layer of insulation,

= 0.0646 X (2????)

Percentage increase in heat loss

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 13

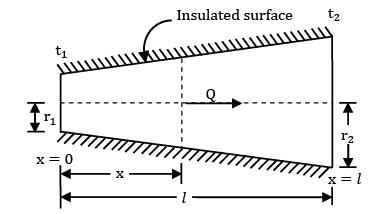
A tapered stainless steel rod, perfectly insulated on the curved surface, has end diameters of 6 cm and 12 cm respectively, and is 20 cm long. The thicker end is fixed to a hot wall and the thinner end is maintained at 25°C. The steady state rate of heat loss through the rod is estimated to be 50W. Calculate the temperature at the hot end of the rod. Take thermal conductivity of the rod material as 15 W/m-°C

Detailed Solution for Test: Conduction Level - 3 - Question 13

The perfectly insulated curved surface implies that the situation corresponds to one-dimensional conduction in the x-direction only for which

Where A_x is the cross-sectional area at any axial position x from the thinner end of the rod.

Radius at distance x:

Then

Separating the variables and upon integration,

we get

Putting the value of in the above expression,

Refer figure

r₁ = 3 cm;r₂ = 6 cm;t₁ = 25°C

The heat flow is from thicker to thinner end

and so Q = -50 W

Substituting the given data in the expression

derived above,

Test: Conduction Level - 3 - Question 14

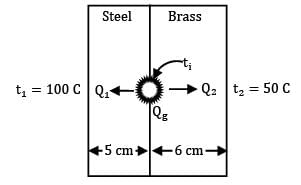
A composite slab consists of a 5 cm thick layer of steel (k = 146 kJ/m-hr-°C) on the left side and a 6 cm thick layer of brass (k = 276 kJ/m-hr-°C) on the right hand side. The outer surfaces of the steel and brass layer are maintained at 100°C and 50°C respectively. The contact between the two slabs is perfect and heat is generated at the rate of 4.2 X 10⁵kJ/m²-hr at the plane of contact. The heat thus generated is dissipated from both sides of composite slab for steady state conditions to calculate heat flow rate through steel and brass slab respectively in MJ/m²-hr.

A. 364.19 & 73.76
B. 364.19 & 364.19
C. 73.76 & 364.19
D. 73.76 & 73.76

Detailed Solution for Test: Conduction Level - 3 - Question 14

Let t_i be the temperature at the interface.

Under stipulation for heat dissipation from

both sides,

t_i >t₁>t₂

Accordingly we may write

Considering unit surface area

= 4.2 X 10⁵

Or 2920 (t_i - 100) + 4600 (t_i - 50)

= 4.2 X 10⁵

or 7520 t_i = 4.2 X 10⁵+ 2.92 X 10⁵ + 2.3 X 10⁵

= 9.42 X 10⁵

∴ Temperature at the interface,

Heat transfer through the steel layer,

= 73759 kJ/m²-hr

Heat transfer through the brass layer,

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 15

A stainless steel wire (thermal conductivity = 20 W/m²°C) & resistivity = 70 micro ohm-cm) of length 2 m and diameter 2.5 mm is submerged in a fluid 50°C at and an electric current of intensity 300 amps passes through it. If heat convection coefficient at the wire surface is 4 kW/m²°C, workout the steady state temperature at the center.

Detailed Solution for Test: Conduction Level - 3 - Question 15

Electrical resistance of wire,

Here generated,

= I²R_s = 300² X 0.285 Watt

Volume of wire, V

= 9.81 X 10^-6m³

Heat generated per unit volume,q_g

= 2.615 X 10⁹ W/m³

Radius of wire, R

The wire surface temperature is given by,

= 50 + 408.59 = 458.59°C

Maximum temperature in the wire occurs at its geometric center line, and can be computed from the relation,

= 458.59 + 51.07 = 510.66°C

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 16

A steel tube of length 20 cm with internal and external diameters of 10 and 12 cm is quenched from 500°C to 30°C in a large reservoir of water at 10°C. Below 100°C the heat transfer coefficient is 1.5 kW/m²K. Above 100°C it is less owing to a film of vapour being produced at the surface, and an effective mean value between 500°C & 100°C is 0.5 kW/m²K.The density of steel is 7500 kg/m³ and the specific heat is 0.47 kJ/kg-K. Neglecting internal thermal resistance of the steel tube, determine the quenching time.

Detailed Solution for Test: Conduction Level - 3 - Question 16

d_i = 10 cm,d_o = 12 cm, ? = 20 cm, T_∞ = 10°C

= 691 cm³

Cooling from 500°C to 100°C

∴ t = 62.12 s

Cooling from 100°C to 30°C

∴ t = 18.35 s

Total time for quenching = 62.12 + 18.38 = 80.5 s

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 17

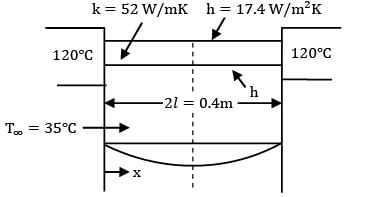
A 50 mm X 50 mm iron bar 0.4 m long is connected to the walls of two heated reservoirs, each at 120°C. The ambient air temperature is 35°C and the convective heat transfer coefficient is 17.4 W/m²-K. Calculate the rate of heat loss from the bar. The thermal conductivity of iron is 52W/m-K.

Detailed Solution for Test: Conduction Level - 3 - Question 17

Because of symmetry, we would consider half-length of the bar (figure).

P = 2(a+b) = 2(50 + 50) = 200 mm = 0.2 m

A = 50 mm X 50 mm = 2500 mm² X 10^-6

= 25 X 10^-4m²

= 5.174m^-1

ml = 5.174 X 0.2 = 1.0348

Tanh ml = 0.776

= 5.174 X 52 X 0.0025 X (120 - 35 ) X 0.776

= 44.37 W

Rate of heat loss from the bar is

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 18

A copper rod (k = 0.15 W/m-°C) is 12 mm in diameter and spans between two plates 150 mm apart. Air flows over the plates providing convective heat transfer coefficient equal to 50 W/m²-°C. If surface temperature of the plates exceeds the air temperature by 45°C, calculate excess temperature at mid length of the rod over that of air. The temperature within the rod varies only along its length.

Detailed Solution for Test: Conduction Level - 3 - Question 18

For a circular rod of diameter d,

Ml = 13.245 X 0.15 ≃ 1.987

Temperature distribution along the length of the bar is given by,

θ ₁ = θ₂ as both the plates are at the same temperature. Temperature excess at the middle of the bar is then obtained by substituting θ₁ = θ₂ and x = 1/2 in the above identity

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 19

During heat treatment, cylindrical pieces of 25 mm diameter, 30 mm height and at 30°C are placed in a furnace at 750°C with convection coefficient 80 W/m²-°C. It is required to heat the pieces to 600°C before pieces are taken out. What will be the shortfall in temperature if the pieces are taken out from the furnace after 280 seconds? Assume the following property values:

Density 7850 kg/m³ ; specific heat 480 J/kg-K; Conductivity 40 W/m-°C

Detailed Solution for Test: Conduction Level - 3 - Question 19

For a cylindrical piece, the characteristic linear dimension is

= 4.41 X 10^-3m

Biot number B_i

= 0.00882 < />

Since B_i < 0.1,the="" lumped="" parameter="" model="" can="" be="" adopted.="" />

= 0.004814

= log_e4.8 = 1.5686

∴ Time required for heating,t

Let T be the temperature attained when the pieces are taken out from the furnace after 280 seconds. Then

∴ Shortfall in temperature

= 600 - 563 = 37°C

*Answer can only contain numeric values

Test: Conduction Level - 3 - Question 20

An egg with a mean diameter of 4 cm and initially at 25°C is placed in a boiling water pan for 4 minutes and found to be boiled to the consumer’s taste. For how long (in seconds) should a similar egg for the same consumer be boiled when taken from a refrigerator at 5°C? Use lumped parameter theory and presume the following properties for egg

k = 12 W/m-°C

h = 125 W/m²-°C

c = 2kJ/kg-K

And ? = 1250 kg/m³

Detailed Solution for Test: Conduction Level - 3 - Question 20

Characteristic length l

Biot number B_i

Since Biot number is less than 0.1, the solution can be worked out by applying lumped-parameter theory which states that

= 0.0075

Let T_a= temperature of boiling water in pan

= 100°C

Now, we have to find time for the temperature values

T_i = 5°C;T_a = 100°C and t = 87.6°C

Or 0.0075 t = log_e7.66 = 2.036

= 271.47 s

	Heat Transfer 57 videos\|77 docs\|86 tests

Heat Transfer

57 videos|77 docs|86 tests

Join Course

Information about Test: Conduction Level - 3 Page

In this test you can find the Exam questions for Test: Conduction Level - 3 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Conduction Level - 3, EduRev gives you an ample number of Online tests for practice

Top Courses for Mechanical Engineering

	Heat Transfer 57 videos\|77 docs\|86 tests

Heat Transfer

57 videos|77 docs|86 tests

Join Course

Top Courses for Mechanical Engineering

Important Questions for Conduction Level - 3

Find all the important questions for Conduction Level - 3 at EduRev.Get fully prepared for Conduction Level - 3 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Conduction Level - 3 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Conduction Level - 3 resources.

Conduction Level - 3 MCQs with Answers

Prepare for the Conduction Level - 3 within the Mechanical Engineering exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Conduction Level - 3 Heat Transfer

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Conduction Level - 3 with ease. Join thousands of successful students who have benefited from our trusted online resources.

Education Revolution