Test: Context Free Grammar - Computer Science Engineering (CSE) MCQ
10 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Context Free Grammar
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Which among the following cannot be accepted by a regular grammar?
For S->0S1|e for ∑={0,1}*, which of the following is wrong for the language produced?
Which of the following is sufficient to convert an arbitrary Context Free Grammar (CFG) to an LL(1) grammar?
To derive the string length 4, How many minimum productions are required for Chomsky normal form ?
A student wrote two context-free grammars G1 and G2 for generating a single C-like array declaration. The dimension of the array is at least one. For example,
int a[10] [3] ;
The grammars use D as the start symbol, and use six terminal symbols int; id[ ] num
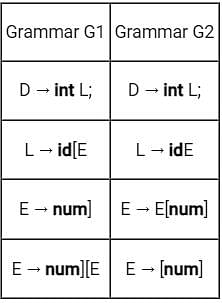
Which of the grammars correctly generate the declaration mentioned above?
Consider the following context-free grammar over the alphabet ∑ = {a, b, c} with S as the start symbol:
S → abScT | abcT
T → bT | b
Which one of the following represents the language generated by the above grammar?
Consider the following languages.
L1 = {wxyx | w, x, y ϵ (0 + 1)+}
L2 = {xy | x, y ϵ (a + b)*, |x| = |y|, x ≠ y}
Which one of the following is TRUE?
|
63 videos|8 docs|165 tests
|
|
63 videos|8 docs|165 tests
|