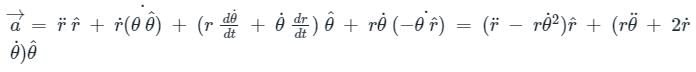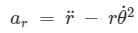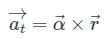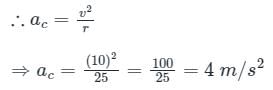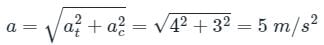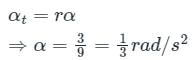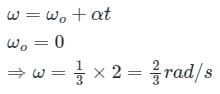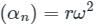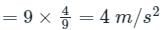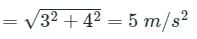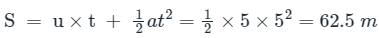Test: Curvilinear Motion - Civil Engineering (CE) MCQ
7 Questions MCQ Test - Test: Curvilinear Motion
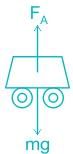
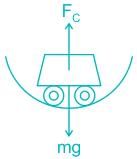
Three identical cars A, B, and C are moving at the same speed on three bridges. Car A moves on a plane bridge, B on a convex bridge, and C on a concave bridge. FA, FB, and FC are the normal forces extorted by the cars on the bridges, then we can say that
The radial component of velocity and acceleration in curvilinear motion are
The speed of a shaft increases uniformly from 300 rpm to 800 rpm in 10 s. The angular acceleration is
The radial component of velocity and acceleration in curvilinear motion are
A body moves with a speed of 10 m/s in the curved path of 25 m radius of curvature. If the tangential acceleration is 3 m/s2, then total acceleration for the body will be:
A car travels on a horizontal circular track of radius 9 m, starting from rest at a constant tangential acceleration of 3 m/s2. What is the resultant acceleration of the car, 2 sec after starting?
The midpoint of a rigid link of a mechanism moves as a translation along a straight line, from rest, with a constant acceleration of 5 m/s2. The distance covered by the said midpoint in 5 s of motion is


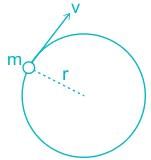

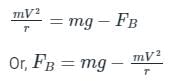

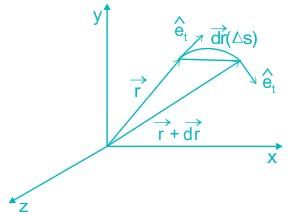
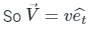

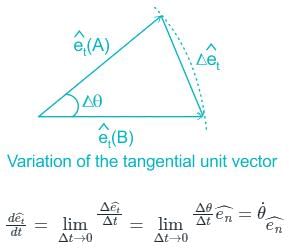

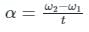

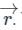 These components are called:
These components are called:

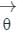
 are represented by
are represented by  respectively. Here A1A2 and B1B2 are perpendicular to the x-axis and are drawn from the endpoints A1 and B1 of the unit vectors
respectively. Here A1A2 and B1B2 are perpendicular to the x-axis and are drawn from the endpoints A1 and B1 of the unit vectors  respectivel
respectivel
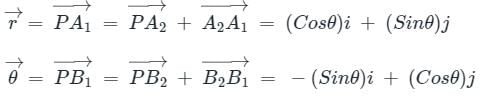
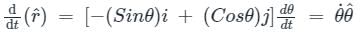
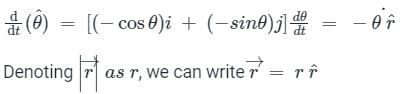
 , the velocity vector is defined as
, the velocity vector is defined as
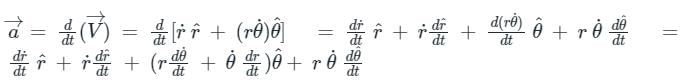
 in acceleration.
in acceleration.