Test: Elementary Mathematics - 7 - CDS MCQ
30 Questions MCQ Test - Test: Elementary Mathematics - 7
Directions: The given equation is 
Which of the following is the value of the given equation?

If (log2 8) + (log2 4) + (log4 2048) + (log2 1024) = 10 + (log5 15625) + (log3 729) + (log8 x), then find the value of x.
A toy weighing 24 grams is an alloy of two metals and is worth Rs. 174. If the weights of the metals in the alloy are interchanged, then the toy would be of worth Rs. 162. Find the price of the other metal in the alloy used to make the toy, if the price of one metal is Rs. 8 per gram.
In a triangle ABC, if A – B = π/2, then C + 2B is equal to
Rajendra bought a mobile with 25% discount on the selling price. If the mobile cost him Rs. 4,875, what was the original selling price of the mobile?
A cyclist moves non-stop from A to B, a distance of 14 km, at a certain average speed. If his average speed reduces by 1 km per hour, he takes 20 minutes more to cover the same distance. The original average speed of the cyclist is
If a sum of money at a certain rate of simple interest per year doubles in 5 years and at a different rate of simple interest per year becomes three times in 12 years, then the difference in the two rates of simple interest per year is
In what ratio should water be added to a liquid costing Rs. 12 per litre to make a profit of 25% by selling the diluted liquid at Rs. 13.75 per litre?
(It is to be assumed that it costs nothing to add water)
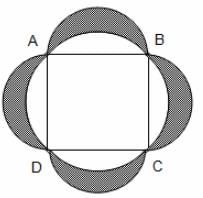
A square ABCD with side 2 units is inscribed in a circle as shown below. Using each side of the square as a diameter, semicircular arcs are drawn. The area of the shaded region outside the circle and inside the semicircles is _____.
If we divide a two-digit number by a number consisting of the same digits written in the reverse order, we get 1 as a quotient and 18 as a remainder. If we add 33 in the given number, we get the sum of the squares of the digits constituting that number. Find the number.
A man travelled 12 km at a speed of 4 km/hr and further 10 km at a speed of 5 km/hr. What was his average speed?
The geometric mean of x and y is 6 and the geometric mean of x, y and z is also 6. Then, the value of z is
The heights (in cm) of five students are 150, 165, 161, 144 and 155. What are the values of mean and median (in cm), respectively?
The difference between two positive numbers is 16. What is the value of the smaller number if it is 3th/5 of the larger number?
The pie diagrams on the monthly expenditure of two families A and B are drawn with radii of two circles taken in the ratio 16 : 9 to compare their expenditures.
Which of the following is the appropriate data used for the above mentioned pie diagrams?
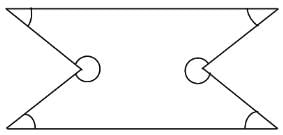
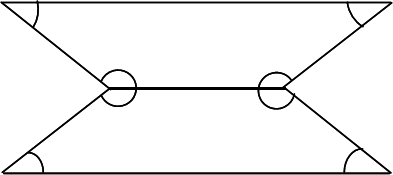
What is the sum of the interior angles of the polygon shown below?
For what value of k does the pair of linear equations given below not have a unique solution?
2x - ky = k - 1
3x - 15y = 2k - 7
If a% of a + b% of b = 2% of ab, then what percent of a is b?
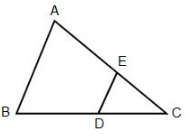
Directions: In triangle ABC, BD = 2DC. Segment ED is parallel to AB. The area of quadrilateral ABDE is 64 sq. cm.
What is the area of triangle EDC?
The average height of 22 students of a class is 140 cm and the average height of 28 students of another class is 152 cm. What is the average height of students of both the classes?
The sum of zeros, the product of zeros, and the sum of the product of zeros taken two at a time of the polynomial x3 + bx2 + cx + d are 3, -24 and -10, respectively. What are the respective values of b, c and d?
On solving the linear equations ax + by + c = 0 and px + my + n = 0, the denominator of x and y is equal to
A thief is spotted by a policeman from a distance of 100 m. When the policeman starts the chase, the thief also starts running. If the speed of the thief is 8 km/hour and that of the policeman is 10 km/hour, then how far will the thief have run before he is overtaken?
If tanθ + cotθ = 4/√3, where 0 < θ < π/2, then sinθ+ cosθ is equal to
Directions: In triangle ABC, BD = 2DC. Segment ED is parallel to AB. The area of quadrilateral ABDE is 64 sq. cm.
What is the ratio of the area of triangle ABC to the area of triangle EDC?


 )(1 +
)(1 +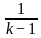 )(1 +
)(1 +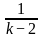 )(1 +
)(1 +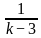 )
)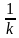 ) = (
) = (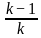 )
)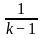 ) = (
) = (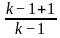 )
)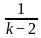 ) = (
) = (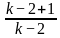 )
)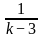 ) = (
) = (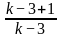 )
)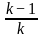 )(
)( )(
)( )(
)(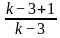 )
)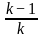 )(
)(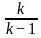 )(
)(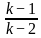 )(
)(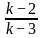 )
)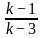 )
)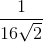

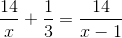
 π sq. units. In total, the four semicircles have an area of 2π sq. units. Thus, the shaded area has an area of 2π - (2π - 4) = 4 sq. units.
π sq. units. In total, the four semicircles have an area of 2π sq. units. Thus, the shaded area has an area of 2π - (2π - 4) = 4 sq. units.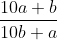
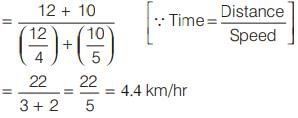
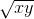 = 6
= 6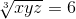
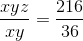
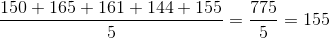
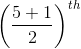 observation = 3rd observation = 155
observation = 3rd observation = 155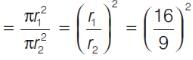
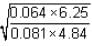 equal to?
equal to?
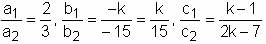


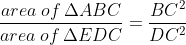
 = 9
= 9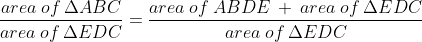 = 9
= 9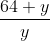 = 9 {Here, y sq. cm = area of triangle EDC}
= 9 {Here, y sq. cm = area of triangle EDC}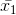 and
and 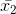 are the respective means (average) of n1 and n2 observations, then the combined mean (average) is:
are the respective means (average) of n1 and n2 observations, then the combined mean (average) is: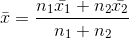
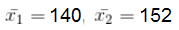
 =
= 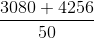 =
= 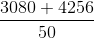 = 146.72 cm
= 146.72 cm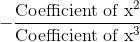
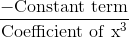
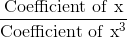
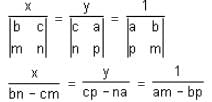
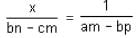
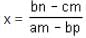

 = 1 ...(1)
= 1 ...(1) = 1 ...(2)
= 1 ...(2)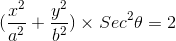
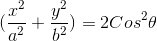
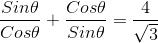
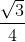
 =
= 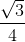
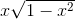 with
with  , we get x =
, we get x = 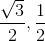 .
.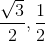
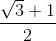 (For both values of x).
(For both values of x).
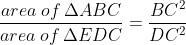
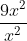 = 9
= 9










