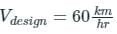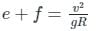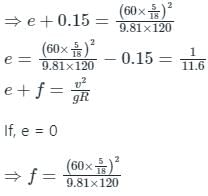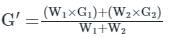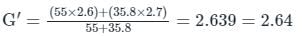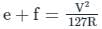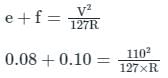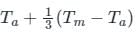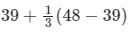Test: Highway Transportation- 2 - Civil Engineering (CE) MCQ
25 Questions MCQ Test - Test: Highway Transportation- 2
The minimum value of camber provided for thin bituminous surface hill roads, is
The minimum value of camber provided for thin bituminous surface hill roads, is
Width of formation for village roads in mountainous areas is
Minimum right of way required for a village road in open area is
Recommended right of way for highways in open areas is
For finding stopping distance of a vehicle, the height of line of sight of driver and height of line of obstacle on road are taken as_____respectively.
Determine the safe stopping speed distance for a design speed of 14 m/s for two-way traffic on a two-lane road assuming the coefficient of friction as 0.28 and reaction time as 2 seconds.
If speed of vehicle is about 100 kmph IRC recommended value of coefficient of friction is
To overtake a vehicle going at 40 kmph on two lane highway OSD is
To overtake a vehicle going at 80 kmph on a two-lane highway overtaking sight distance is
Sight distance at intersection should be equal to
Sight distance at intersection should be at least along the minor road.
If design speed of a main road is 100 kmph, the sight distance at intersection should be at least
If the cross slope of terrain is 15, it is classified as
The radius of a horizontal circular curve on a highway is 120 m. The design speed is 60 km/hour, and the design coefficient of lateral friction between the tyre and the road surface is 0.15. The estimated value of superelevation required (if full lateral friction is assumed to develop), and the value of coefficient of friction needed (if no superrelevation is provided) will, respectively, be
In Marshall method of mix design, the coarse aggregate, fine aggregate, fines and bitumen having respective values of specific gravity 2.60, 2.70, 2.65 and 1.01, are mixed in the relative proportions (% by weight) of 55.0, 35.8, 3.7 and 5.5 respectively. The theoretical specific gravity of the mix and the effective specific gravity of the aggregates in the mix respectively are:
When a vehicle weighing W traces a horizontal curve of radius R with uniform velocity v it is
subjected to a centrifugal force
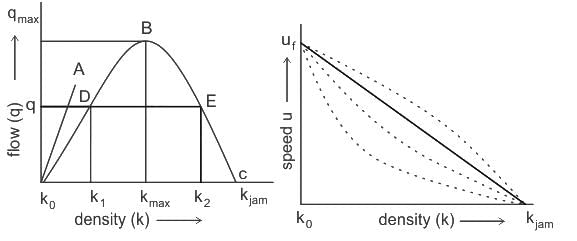
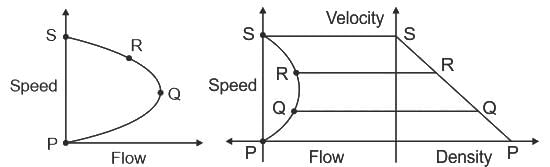
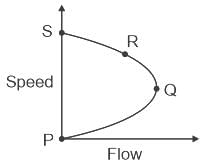
Consider the four points P, Q, R, and S shown in the Greenshields fundamental speed-flow diagram. Denote their corresponding traffic densities by kp, kQ, kR, and ks , respectively. The correct order of these densities is
A road is being designed for a speed of 110 km/hr on a horizontal curve with a super elevation of 8%. If the coefficient of side friction is 0.10, the minimum radius of the curve (in m) required for safe vehicular movement is
A vehicle weighs 50 kN when empty. Its minimum velocity for skidding on a curve is v. If it is weighing 100 kN so that centroid remains at the same height when loaded, it; minimum velocity for skidding on a curve is
For the hottest month of the year at the proposed airport site, the monthly mean of the average daily temperature is 390C. The monthly of the maximum daily temperature is 480C for the same month of the year. From the given information, the calculated Airport Reference Temperature (in 0C), is
The value of ruling gradient in hills, as recommended by Indian Road Congress, is: