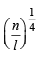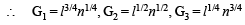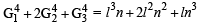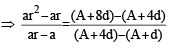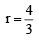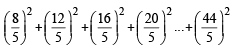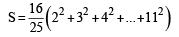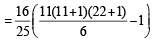Test: JEE Main 35 Year PYQs- Sequences & Series - JEE MCQ
30 Questions MCQ Test - Test: JEE Main 35 Year PYQs- Sequences & Series
If 1, log9 (31–x + 2), log3 (4.3x – 1) are in A.P. then x equals [2002]
l, m, n are the pth, qth and rth term of a G. P. all positive, then  equals[2002]
equals[2002]
 equals[2002]
equals[2002]The value of 21/4. 41/8. 81/16 ... ∞ is [2002]
4. Fifth term of a GP is 2, then the product of its 9 terms is [2002]
Sum of infinite number of terms of GP is 20 and sum of their square is 100. The common ratio of GP is [2002]
13 – 23 + 33 – 43 +...+93 = [2002]
The sum of the series [2003]
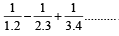 up to ∞ is equal to
up to ∞ is equal to
Let Tr be the rth term of an A.P. whose first term is a and common difference is d. If for some positive integers
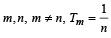 and
and 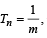 , then a – d equals [2004]
, then a – d equals [2004]
The sum of the first n terms of the series
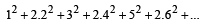 is
is 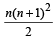 when n is even. When n is odd the sum is [2004]
when n is even. When n is odd the sum is [2004]
If the coefficients of r th, (r + 1)th, and (r + 2)th terms in the the binomial expansion of (1 + y)m are in A.P., then m and r satisfy the equation [2005]
IF 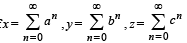 where a, b, c are in AA..PP and |a | < 1, | b | < 1, | c | < 1 then x, y, z ar e in [2005]
where a, b, c are in AA..PP and |a | < 1, | b | < 1, | c | < 1 then x, y, z ar e in [2005]
The sum of the series [2005]
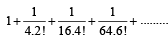 .................ad inf. is
.................ad inf. is
Let a1,a2 ,a3 ............ be terms on A.P. If 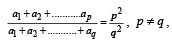 then
then 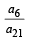 equals [2006]
equals [2006]
If a1 , a2 , ........,an are in H.P., then the expression a1a2 + a2 a3 + ..........+ an -1an is equal to [2006]
The sum of series 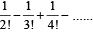 ... upto infinity is [2007]
... upto infinity is [2007]
In a geometric progression consisting of positive terms, each term equals the sum of the next two terms. Then the common ratio of its progression is equals [2007]
The first two terms of a geometric progression add up to 12. the sum of the third and the fourth terms is 48. If the terms of the geometric progression are alternately positive and negative, then the first term is [2008]
The sum to infinite term of the series 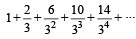 [2009]
[2009]
A person is to count 4500 currency notes. Let an denote the number of notes he counts in the nth minute. If a1 = a2 = ... = a10 = 150 and a10, a11, ... are in an AP with common difference –2, then the time taken by him to count all notes is [2010]
A man saves 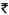 200 in each of the first three months of his service. In each of the subsequent months his saving increases by
200 in each of the first three months of his service. In each of the subsequent months his saving increases by 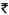 40 more than the saving of immediately previous month. His total saving from the start of service will be
40 more than the saving of immediately previous month. His total saving from the start of service will be 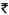 11040 after [2011]
11040 after [2011]
Statement-1: The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + .... + (361 + 380 + 400) is 8000
Statement-2: 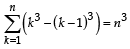 for any natural number n. [2012]
for any natural number n. [2012]
The sum of first 20 terms of the sequence 0.7, 0.77, 0.777,....., is [JEE M 2013]
If (10)9 + 2(11)1 (108) + 3(11)2 (10)7 + K........ +10 (11)9 = k (10)9, then k is equal to: [JEE M 2014]
Three positive numbers form an increasing G. P. If the middle term in this G.P. is doubled, the new numbers are in A.P. then the common ratio of the G.P. is: [JEE M 2014]
The sum of first 9 terms of the series. 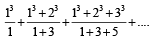 [JEE M 2015]
[JEE M 2015]
If m is the A.M. of two distinct real numbers l and n(l, n > 1) and G1, G2 and G3 are three geometric means between l and n, then 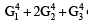 equals : [JEE M 2015]
equals : [JEE M 2015]
If the 2nd, 5th and 9th terms of a non-constant A.P. are in G.P., then the common ratio of this G.P. is : [JEE M 2016]
If th e sum of th e fir st ten ter ms of th e series
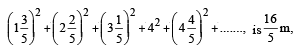
then m is equal to : [JEE M 2016]


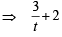 =
= 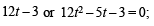
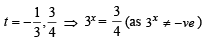
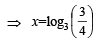 or x = log33 – log3 4
or x = log33 – log3 4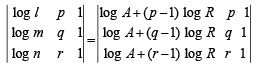
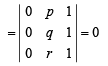

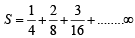 ......(1)
......(1)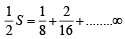 ......(2)
......(2)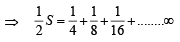
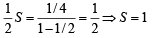
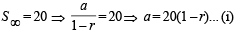
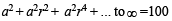
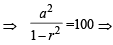 a2 = 100(1 – r)(1 + r)... (ii)
a2 = 100(1 – r)(1 + r)... (ii)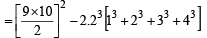
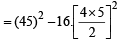 = 2025 – 1600 = 425
= 2025 – 1600 = 425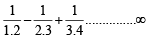
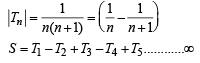
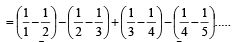
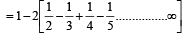
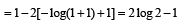
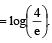

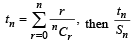 is equal to
is equal to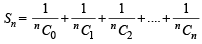
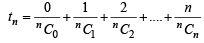
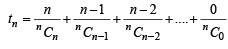
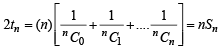
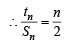
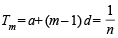 ............(1)
............(1)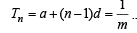 ..............(2)
..............(2)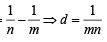
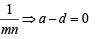
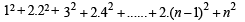
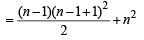
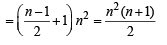
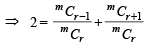
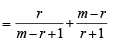
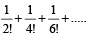 is [2004]
is [2004]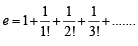
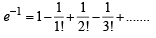
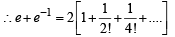
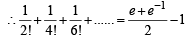
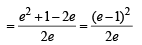
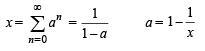
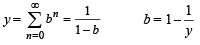
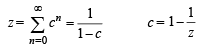
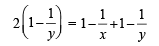
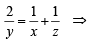 x, y, z are in H.P..
x, y, z are in H.P..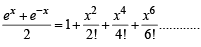
 we get
we get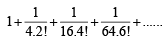
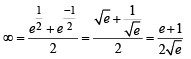
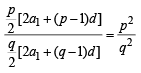
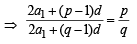
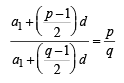
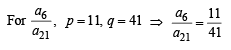
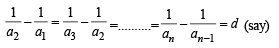
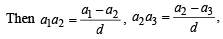
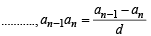
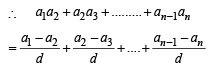
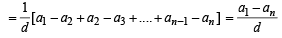
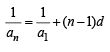
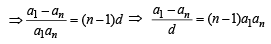
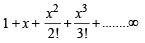
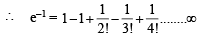
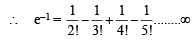
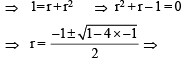
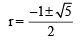
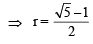 [∵ terms of G.P. are positive
[∵ terms of G.P. are positive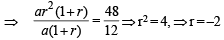
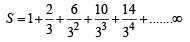 ....(1)
....(1)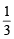 we get
we get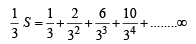 ....(2)
....(2)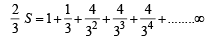
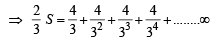
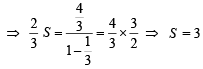
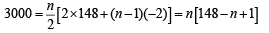
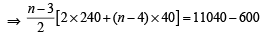
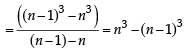
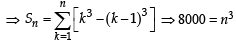
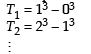
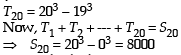
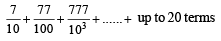
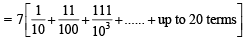
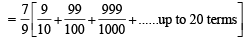
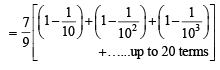
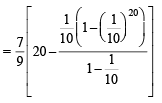
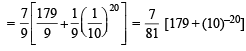
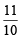 on both the sides
on both the sides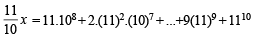
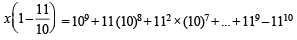
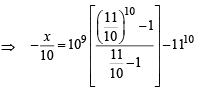
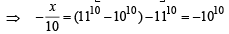
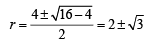
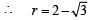 is rejected
is rejected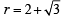
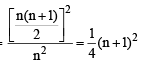
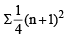
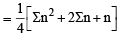
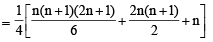
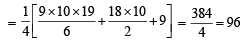
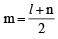 and common ratio of G.P. = r =
and common ratio of G.P. = r =