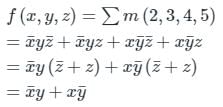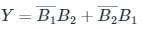Test: K-Map - 2 - Electrical Engineering (EE) MCQ
15 Questions MCQ Test - Test: K-Map - 2
If we group four 1’s from the adjacent cells of a K-map, then the group is called:
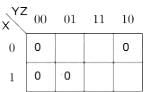
In the sum of products function (X, Y, Z) = ∑(2, 3, 4, 5), the prime implicants are
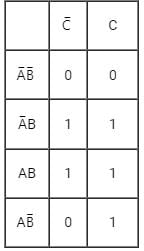
Which of the following is the Boolean function for Majority Voting, assuming A, B, C are inputs and Y is output?
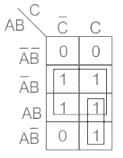
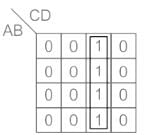
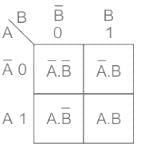
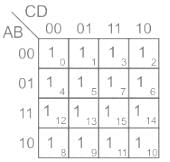
What is the simplest expression for the K-map shown in the table given below?
A boolean function is given as F(x, y, z) = ∑(1, 3, 6, 7). What is its equivalent canonical form?
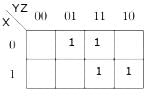
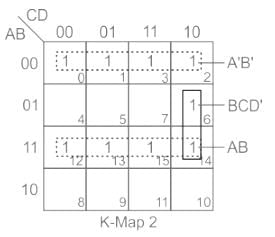
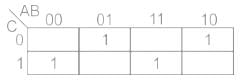
Which is the simplified expression for the output corresponding to the given K map?
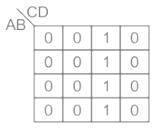
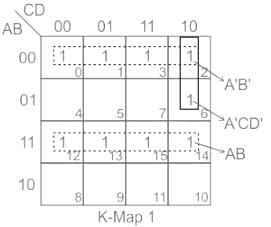
Simplified expression/s for following Boolean function F(A, B, C, D) = ∑ (0, 1, 2, 3, 6, 12, 13, 14, 15) is/are
(A) A'B' + AB + A'C'D'
(B) A'B' + AB + A'CD'
(C) A'B' + AB + BC'D'
(D) A'B' + AB + BCD'
Choose the correct answer from the options given below:
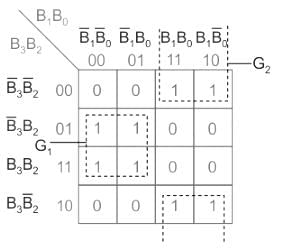
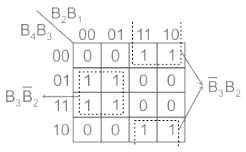
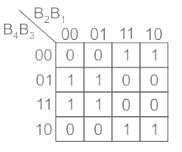
The K-map given below represents the bit G2 for a 4-bit Binary (B4B3B2B1) to Gray (G4G3G2G1) converter. What will be the expression of G2?
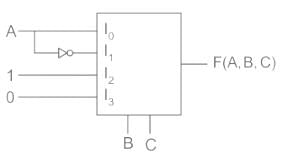
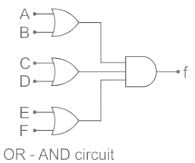
A 4 × 1 MUX used to implement a 3-input Boolean function is as shown above. The Boolean function F(A, B, C) implemented is:
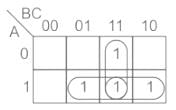
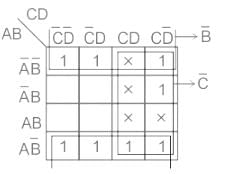
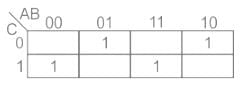
A combination circuit has inputs A, B and C, its K-map is given below. The output of circuit is given by
Simplify the Boolean expression:
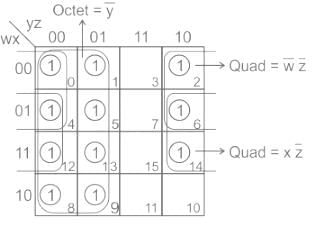
F(w,x,y,z) = ∑ (0,1,2,4,5,6,8,9,12,13,14)
Given f(A, B, C, D) = ∑ m(0, 1, 2, 6, 8, 9, 10, 11) + ∑ d(3, 7, 14, 15) is a Boolean function, where m represents min-terms and d represents don’t cares. The minimal sum of products expression for f is