Test: Kinematic Indeterminacy - Civil Engineering (CE) MCQ
10 Questions MCQ Test Structural Analysis - Test: Kinematic Indeterminacy
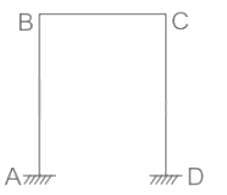
A single-bay, single-storeyed portal frame ABCD has its column ends fixed. If axial deformation is neglected, the kinematic indeterminacy is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A continuous beam ABC with span AB = BC = L is shown in the figure. Supports A is fixed type, and supports B and C are roller type. The kinematic indeterminacy of the beam is:


What is the degree of kinematic indeterminacy of the beam shown in figure above
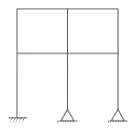
What is the number of kinematic indeterminacy for the building frame as shown in the figure when members are inextensible:

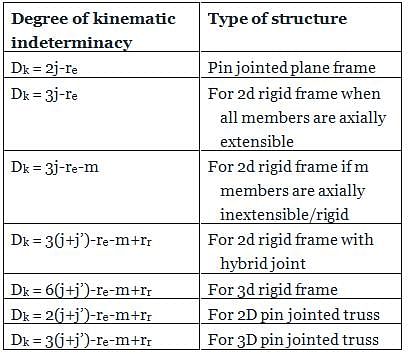
Degree of kinematic indeterminacy of a pin jointed plane frame is given by
A singly-bay single-storeyed portal frame ABCD is fixed at A and D as shown in the figure. If axial deformation is neglected, the kinematic indeterminacy is

For the plane frame as shown in the figure
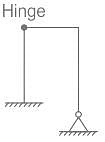
The degree of kinematic indeterminacy, neglecting axial deformation, is
The kinematic indeterminacy of the following beam after imposing the boundary
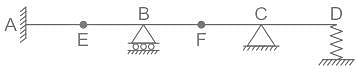

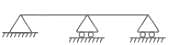
Find the degree of static indeterminacy, for a two dimensional truss (or frame) shown in the figure above.
|
34 videos|140 docs|31 tests
|
|
34 videos|140 docs|31 tests
|