Commerce Exam > Commerce Tests > Mathematics (Maths) Class 11 > Test: Limits And Derivatives - 1 - Commerce MCQ
Test: Limits And Derivatives - 1 - Commerce MCQ
Test Description
25 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Limits And Derivatives - 1
Test: Limits And Derivatives - 1 for Commerce 2024 is part of Mathematics (Maths) Class 11 preparation. The Test: Limits And Derivatives - 1 questions and answers have been
prepared according to the Commerce exam syllabus.The Test: Limits And Derivatives - 1 MCQs are made for Commerce 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Limits And Derivatives - 1 below.
Solutions of Test: Limits And Derivatives - 1 questions in English are available as part of our Mathematics (Maths) Class 11 for Commerce & Test: Limits And Derivatives - 1 solutions in
Hindi for Mathematics (Maths) Class 11 course. Download more important topics, notes, lectures and mock
test series for Commerce Exam by signing up for free. Attempt Test: Limits And Derivatives - 1 | 25 questions in 25 minutes | Mock test for Commerce preparation | Free important questions MCQ to study Mathematics (Maths) Class 11 for Commerce Exam | Download free PDF with solutions
Detailed Solution for Test: Limits And Derivatives - 1 - Question 1
Detailed Solution for Test: Limits And Derivatives - 1 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Test: Limits And Derivatives - 1 - Question 3
Let f (x) = x sin 1/x, x ≠ 0, then the value of the function at x = 0, so that f is continuous at x = 0, is
Detailed Solution for Test: Limits And Derivatives - 1 - Question 3
Test: Limits And Derivatives - 1 - Question 4
The positive integer n so that limx→3 (xn – 3n)/(x – 3) = 108 is
Detailed Solution for Test: Limits And Derivatives - 1 - Question 4
Detailed Solution for Test: Limits And Derivatives - 1 - Question 5
Detailed Solution for Test: Limits And Derivatives - 1 - Question 7
Detailed Solution for Test: Limits And Derivatives - 1 - Question 8
Detailed Solution for Test: Limits And Derivatives - 1 - Question 9
Detailed Solution for Test: Limits And Derivatives - 1 - Question 10
Detailed Solution for Test: Limits And Derivatives - 1 - Question 11
Test: Limits And Derivatives - 1 - Question 12
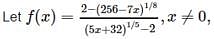 then for f to be continuous at x = 0, f (0) must be equal to
then for f to be continuous at x = 0, f (0) must be equal to
Detailed Solution for Test: Limits And Derivatives - 1 - Question 12
Detailed Solution for Test: Limits And Derivatives - 1 - Question 17
Detailed Solution for Test: Limits And Derivatives - 1 - Question 19
Detailed Solution for Test: Limits And Derivatives - 1 - Question 20
Detailed Solution for Test: Limits And Derivatives - 1 - Question 23
Detailed Solution for Test: Limits And Derivatives - 1 - Question 25
|
75 videos|238 docs|91 tests
|
Information about Test: Limits And Derivatives - 1 Page
In this test you can find the Exam questions for Test: Limits And Derivatives - 1 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Limits And Derivatives - 1, EduRev gives you an ample number of Online tests for practice
|
75 videos|238 docs|91 tests
|
Download as PDF


 is equal to
is equal to 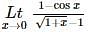 is equal to
is equal to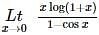 is equal to
is equal to  is equal to
is equal to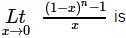
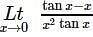 is equal to
is equal to
 is equal to
is equal to  is equal to
is equal to 

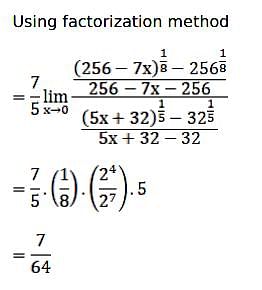

 where a > 0, is equal to
where a > 0, is equal to 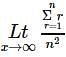 (x=n) , is equal to
(x=n) , is equal to 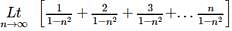 is equal to
is equal to is equal to
is equal to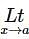

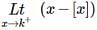 is equal to
is equal to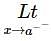
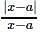 is equal to
is equal to is equal to
is equal to 
 is equal to
is equal to 












